Heat and Mass Transfer 2(2+0)

Lesson-26 Logarithmic mean temperature difference for parallel flow heat exchanger, counter and cross flow heat exchangers, Overall Heat Transfer Coefficient for a Plane wall and Double Pipe Heat Exchanger

 

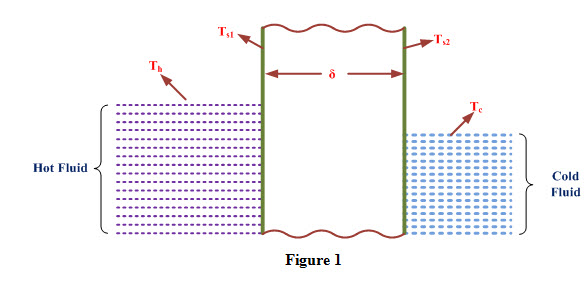
Heat transferred to wall surface by hot fluid is expressed as

Heat transferred through the wall by conduction is expressed as

Heat convected to cold fluid by wall surface is expressed as

Adding both sides of equations (1), (2) and (3), we get

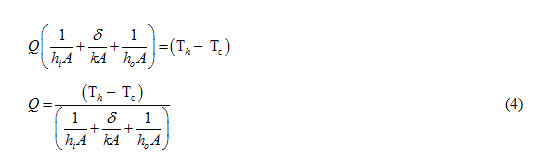
We know that heat transfer in a heat exchanger can be expressed as

Q = UA (T_h – T_c)                                                                                     (5)

Comparing equations (4) and (5), we can write

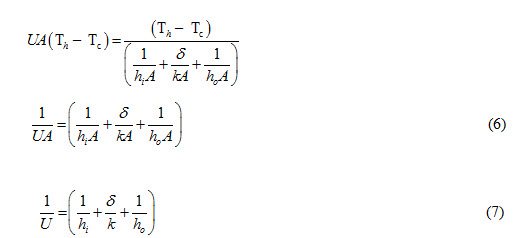
Equation (7) represents overall heat transfer coefficient for aplane wall.

2. Double Pipe Heat Exchanger

Consider a double pipe heat exchanger of length ‘L’ in which hot fluid and cold fluid are flowing through inner and outer pipes respectively as shown in Figure 2.

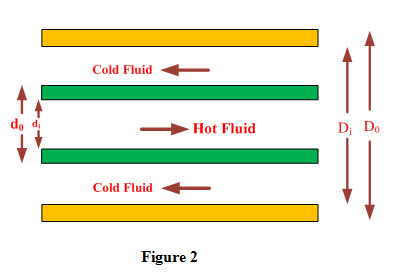
Let

h_i and h_o are convective heat transfer coefficients of hot and cold fluids with pipe surfaces respectively.

d_i and d_o  are inside and outside diameters of inner pipe having thickness ‘δ’ and thermal conductivity ‘k’.

                                       

A_o= Π d_oL and A_i= Π d_iL

D_i and D_o are inside and outside diameters of outer pipe respectively.

Using equation (6), overall heat transfer coefficient, U for the arrangment can be expressed as

Substituting values of A_i , A_o and A_m  in equation (10), we get

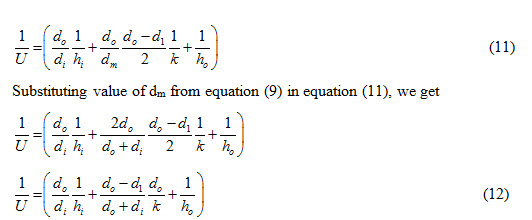
Equation (12) represents overall heat transfer coefficient with reference to outer surface of inner pipe of a double pipe heat exchanger.

Heat Transfer Analysis in Heat Exchanger

Heat is transferred from hot fluid to cold fluid in heat exchanger and it involves the following steps

i)  Heat lost by hot fluid is expressed as

         Q_h = m_h c_ph (T_hi - T_ho)                                                                       (13)

ii)    Heat gained by cold fluid is expressed as

          Q_c = m_c c_pc (T_co – T_ci)                                                                         (14)

iii)   Heat transfer in heat exchanger is expressed as

          Q = U A (ΔT)_m                                                                                                               (15)

From energy balance considerations, heat transferred in heat exchanger is equal to heat lost by hot fluid which is gained by cold fluid.

         Q = Q_h = Q_c                                                                                     (16)

Performance of a heat exchanger can be analyzed by using following methods

1.      Logarithmic Mean Temperature Difference or LMTD Method
2.      Effectiveness of Number of Transfer Unit (NTU) Method

1. Logarithmic Mean Temperature Difference (LMTD) Method:

LMTD method is used when temperatures of both the fluids at inlet and outlet of the heat exchanger are known. Performance analysis by this method is carried out by making following assumptions:

i)        Overall heat transfer coefficient, U remains constant along the length of heat exchanger.

ii)      Specific heats and mass flow rates of both the fluids remain constant.

iii)    Heat exchanger is perfectly insulated and no loss of heat occurs.

iv)    Axial conduction along the pipes is negligible.

A. Parallel Flow Heat Exchanger:

Consider a parallel flow heat exchanger of length ‘L’ as shown in Figure 3 and let m_h and m_c are mass flow rates of hot and cold fluids respectively.

T_hi and T_ho are temperatures of hot fluid at inlet and outlet of heat exchanger respectively.

T_ci and T_co are temperatures of cold fluid at inlet and outlet of heat exchanger respectively

c_ph and c_pc are specific heats of hot and cold fluids respectively.

θ_i and θ_o represent temperature difference between hot and cold fluids at inlet and outlet of heat exchanger respectively and are expressed as

 θ_i = T_hi –T_ci and θo = T_ho –T_co                                                                               (17)

C_h  and C_c  are heat capacity rates of hot and cold fluid respectively.

Heat capacity rate of a fluid is defined as amount of heat required to increase temperature of a fluid by 1 ^oC and is expressed as

  C_h = m_h C_{ph, ,} C_c = m_c C_pc                                                                                    (18)

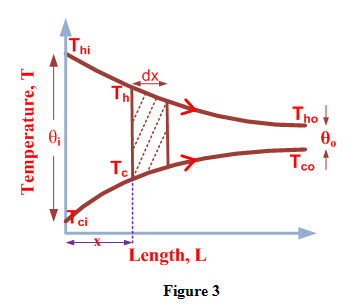
Consider an element of area dA and thickness dx at a distance ‘x’ from inlet of heat exchanger. Let T_h and T_c are temperatures of hot and cold fluid at inlet of the element and θ represents temperature difference of hot and cold fluid at inlet of the element.

         θ = T_h –T_c                                                                                                         (19)

Let dT_h and dT_c represent change in temperature of hot and cold fluids respectively during the flow through the element. Let dθ be the difference in change in temperature of hot and cold fluids during flow through the element and is expressed as

         dθ = dT_h - dT_c                                                                                                   (20)

    During flow through the element, heat transferred is equal to heat lost by hot fluid and heat gained by cold fluid.

If dQ is the amount of heat transferred during flow of fluids through the element then

dQ = UdA θ = m_c c_pc dT_c =  - m_h c_ph dTh                                                                 (21)

 (-ve sign if temperature of fluid decreases along the length of heat exchanger)

Using equation (18), equation (21) can be written as

    dQ = UdA θ = C_c dT_c =  - C_h dTh                                                                         (22)      

From equation (22), we can write

Substituting the values of dT_c and dT_h  from equation (23) in equation (20), we get

Integrating equation (24) between limits θ_i and θ_o­      

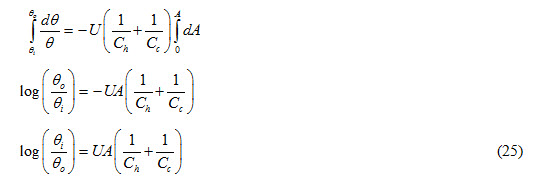
Heat lost by hot fluid during flow through heat exchanger is expressed as

   Q =  m_h c_ph (T_hi – T_ho) = C_h (T_hi – T_ho)

    Therefore,                                              (26)                                                                  

Heat gained by cold fluid during flow through heat exchanger is expressed as

    Q =  m_c c_pc (T_co – T_ci)

     Therefore,                                   (27)                                                                       

Substituting values of C_h and C_c from equations (26) and (27) in equation (25), we get

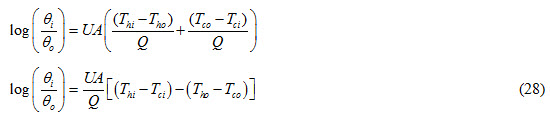
Using equation (17), equation (28) can be written as

Comparing equations (29) and (15), we can write

Equation 24.17 represents logarithmic mean temperature difference for a parallel flow heat exchanger.