Heat and Mass Transfer 2(2+0)

Lesson-28 Heat exchanger performance in terms of Capacity ratio, Effectiveness and Number of transfer units, Effectiveness for parallel flow heat exchanger

Capacity ratio (C): It is defined as ratio of minimum to maximum capacity rate of fluids being used in a heat exchanger.

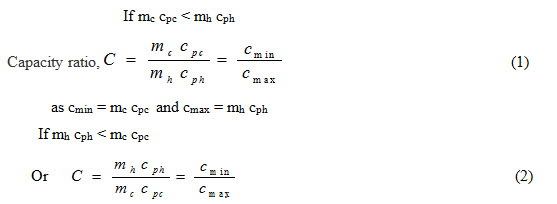
as c_min = m_h c_ph  and c_max = m_c c_pc

The fluid with lower heat capacity rate will undergo greater change in temperature as compared to fluid with higher heat capacity rate.

Effectiveness, ε:

Effectiveness of a heat exchanger is defined as ratio of actual heat transferred to maximum possible heat that can be transferred.

Q_actual = Heat lost by hot fluid = Heat gained by cold fluid

Q_actual = m_h c_ph (T_hi - T_ho)  =  m_c c_pc (T_co – T_ci)                                                     (4)                                                          

Maximum possible heat transfer will be achieved if a fluid undergoes a change in temperature equal to maximum temperature difference available between hot and cold fluid.

Maximum Temperature difference that exists in a heat exchanger = T_hi - T_ci

Maximum possible heat transfer occurs when a fluid of smaller heat capacity rate undergoes a change in temperature equal to maximum available temperature difference.

Q_maxpossibe = C_min (T_hi – T_ci)                                                                           (5)

Substituting values of Q_actual and Q_{max possible} from equations (4) and (5) in equation (3), we get

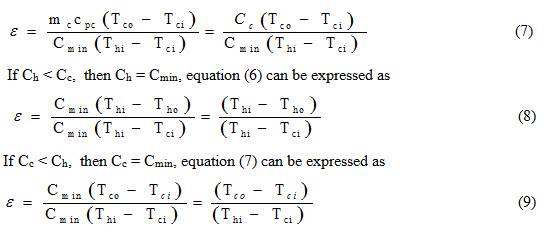
Effectiveness may also be defined as ratio of change in temperature of fluid with smaller capacity rate to maximum temperature difference existing in a heat exchanger.

Number of Transfer Units, NTU:

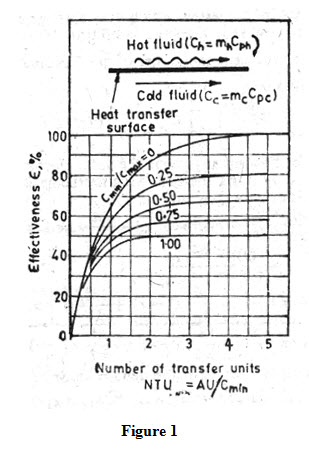
Number of transfer units is a dimensionless quantity and is an indicator of size of heat transferring areas of heat exchanger. Large value of NTU means larger heat transferring area. It is expressed as

(a) Effectiveness for the Parallel Flow Heat Exchangers:

From definition of effectiveness of a heat exchanger, we can write

Heat transferred in a heat exchanger can be expressed as

Q = C_h(T_hi- T_ho) = C_c(T_co-T_ci)   

Consider an element of area dA and thickness dx at a distance ‘x’ from inlet of a parallel flow heat exchanger. Let dT_h and dT_c represent change in temperature of hot and cold fluids respectively during the flow through the element. Temperature difference between hot and cold fluid at inlet of element is expressed as

dθ = dT_h - dT_c                                                                                                    (12)                                                                                      

If dQ is the amount of heat transferred during flow of fluids through the element then

dQ = UdA θ = C_c dT_c =  - C_h dTh                                                                             (13)                                                          

Substituting the values of dT_h and dT_c from equation (13) into the equation (12), we get

                                       

Integrating equation (14) between limits θ_i and θ_o­ , we get  

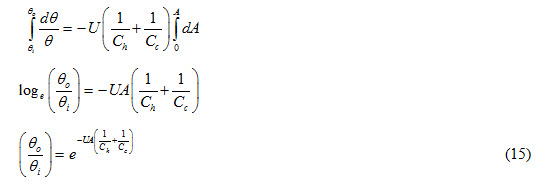
For a parallel heat exchanger,

θ_i = T_hi –T_ci and θo = T_ho –T_co       

Equation (15) can be written as

Using equation (4), values of T_ho and T_co  can be written as                           

Subtracting equation (18) from equation (17), we get

Using equation (19), equation (16) can be written as

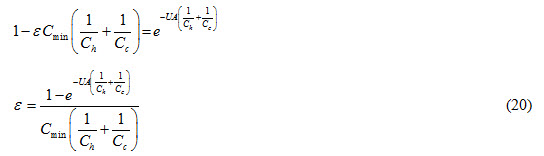
If C_c < C_h,  then C_c = C_min and C_h = C_max equation (20) can be expressed as

If C_h < C_c,  then C_h = C_min and C_c = C_max equation (20) can be expressed as

Using equations (2) and (10), equation (22) can be expressed as

The following two important cases are considered

i) Gas Turbine:

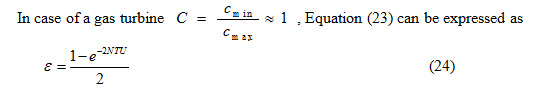
For a parallel flow heat exchanger, maximum value of effectiveness that can be achieved is 50% irrespective of values of its heat transferring area and overall heat transfer coefficient.

ii) Boiler and Condenser: