Theory of Machines

Lesson 5.

5.2 MOTION OF A LINK

Consider a rigid link OA of length r having uniform angular velocity ω rad/s. OA turns through a small angle δθ in small interval of time δt. Then A will travel along arc AA'.

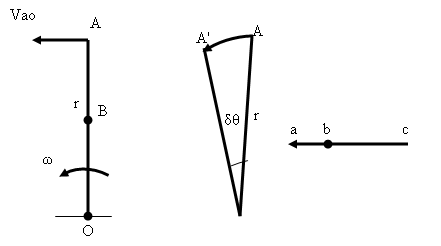
Fig. 3.1 motion of a link

Velocity of A relative to O = Arc AA'/ δt

\[{V_{ao}} = r\frac{{\delta \theta }}{{\delta t}}\]                             

In the limits, when δt tends to zero

\[{V_{ao}} = r\frac{{d\theta }}{{dt}}\]

\[{{\text{V}}_{{\text{ao}}}} = {\text{ r }} \times \omega {\text{ }}\left( {{\text{OA }} \times \omega } \right)\]

The direction of V_ao is along the displacement of A. Also, as δt approaches zero, AA’ will be perpendicular to OA. Thus, velocity of A is ωr and perpendicular to OA. It is so because A can neither approach nor recede from O and thus, the only possible motion of A relative to O is in a direction perpendicular to OA.

Now, consider appoint B o the link OA

The velocity of point B = ω OB which is perpendicular to OB

If ob represents the velocity of B, it can be found that

\[\frac{{{\text{ob}}}}{{{\text{oa}}}} = \frac{{{\text{ }}\omega {\text{OB}}}}{{\omega {\text{ OA}}}} = \frac{{{\text{OB}}}}{{{\text{OA}}}}\] 

The important conclusion here is that b divides the velocity vector in the same ratio as B divides the link. The velocity vector V_ao gives the velocity of A at a particular instant of time at other instant of time when OA takes other position the velocity vector will change its direction accordingly.

5.3 FOUR BAR MECHANISM ANALYSIS BY RELATIVE VELOCITY METHOD

Four bar mechanism is given below in the diagram having angular velocity ω rad/s in the clockwise direction

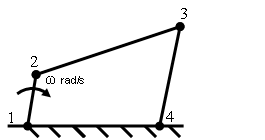
Fig. 3.2 four bar mechanism

Velocity of the point 3 relative to 1= velocity of point 3 relative to velocity of point 2+ velocity of point 2 relative to velocity of point 1.                            

\[{{\text{V}}_{{\text{31}}}} = {{\text{V}}_{{\text{32}}}} + {{\text{V}}_{{\text{21}}}}\]                            

The velocity of point 3 relative to 1 will be equal to velocity of point 3 relative to 4 as point 1 & point 4 both are fixed point, so we can write

\[{{\text{V}}_{{\text{34}}}} = {{\text{V}}_{{\text{32}}}}{\text{ + }}{{\text{V}}_{{\text{21}}}}\]

                         

Here

\[{{\text{V}}_{{\text{21}}}} = \omega\times {\text{12}}\], which is perpendicular to 12

Similarly,

V₃₂ is unknown in magnitude but it will be perpendicular to link 23

V₃₄ is unknown in magnitude but it will be perpendicular to link 43

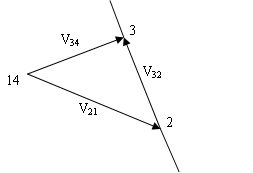
Fig. 3.3

Angular velocity of links

a. Velocity of 3 relative to 2, V₃₂ link 3 moves in anti-clockwise about 2.

\[{{\text{V}}_{{\text{32}}}}{\text{ = }}{\omega _{{\text{32}}}} \times {\text{23}}\]

\[{\omega _{{\text{32}}}} = {\text{ }}\frac{{{{\text{V}}_{{\text{32}}}}}}{{{\text{23}}}}\]

b. Velocity of link 34

Angular velocity of link 3 relative to 4 is in clockwise direction & is given by

\[{\omega _{{\text{34}}}}{\text{ = }}\frac{{{{\text{V}}_{{\text{34}}}}}}{{{\text{43}}}}\]

5.4 VELOCITY OF RUBBING AT PINS

Two links forms a turning pairs at points 1, 2, 3&4 as shown in figure 3.4. It can be seen here that a pin forms an integral part of a link and this pin fits into the hole in the other link which permits the relative motion between them. When two links are connected then the surface at the hole of one link rubs against the surface of pin of the other link. The rubbing velocity between the two links depends on the angular velocity of one link relative to the angular velocity of the other.

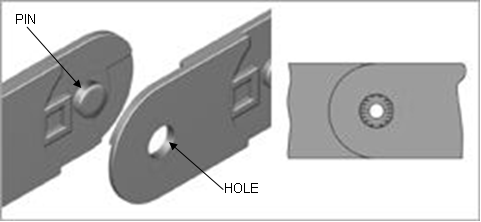Fig.3.4 two links joined by pins

This can be explained at the points 1, 2, 3 & 4 in figure 3.2 of the four bar mechanism.

At pin 1

The pin at 1 connects links 12 and 41, the velocity of rubbing will depend only on links 12 as 41 is the fixed link.

Let \[{r_1}\] = radius of the pin at point 1

Then the velocity of rubbing = \[{r_1} = \omega \]

At pin 2

\[{\omega _{21}} = {\omega _{12}} = \omega \]  clockwise

\[{\omega _{23}} = {\omega _{32}} = \frac{{{V_{23}}}}{{23}}\]  counter clockwise

The direction of the two angular velocities of the links 12 and 23 are in opposite directions, the angular velocity of one link relative to the other is the sum of the two velocities.                                            

Let \[{r_2}\] = radius of the pin at point 2

Then the velocity of rubbing = \[{r_2} = \left( {{\omega _{12}} + {\omega _{23}}} \right)\]

At pin 3

\[{\omega _{23}} = {\omega _{32}}\] counter clockwise

\[{\omega _{41}} = {\omega _{34}}\]  clockwise

Let \[{r_3}\] = radius of the pin at point 3

Then the velocity of rubbing = \[{r_3} = \left( {{\omega _{23}} + {\omega _{43}}} \right)\]

At pin 4

Let \[{r_4}\] = radius of the pin at point 4

Then the velocity of rubbing = \[{r_4} = {\omega _{34}}\]