Theory of Machines

Lesson 7.

Fig. 3.11 Aronhold –Kennedy’s theorem

as shown in the above figure 3.11, the I-centre I₁₃ and I₁₂ are located by observation , then the third I-centre I₂₃ will lie on the line extended from I₁₃ & I₁₂ and cutting the line perpendicular to the velocity .

7.2 METHOD FOR LOCATING I-CENTRE

Step 1. The number of I-centre in a four bar mechanism is

\[n = \frac{{n(n - 1)}}{2}\]

Where n = No. of links

The number of I-centre in a four bar mechanism will be         

\[\frac{{{\text{4}} \times \left( {{\text{4}} - {\text{1}}} \right)}}{{\text{2}}} = {\text{6}}\]                              .

So there are 6 I-centre in a four bar mechanism

Step 2. These I-centre’s is shown below

Links	1	2	3	4
I-centre’s	I12	I23	I34	-
	I13	I24	-	-
	I14	-	-	-

 

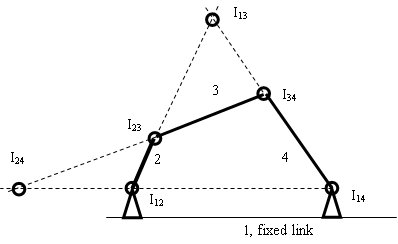
Fig. 3.12

Step 3. I₁₂ and I₁₄ are found to be fixed I-centre because they will change their position during the rotation of crank or at any position of crank. The I₂₃ and I₃₄ are permanent types of I-centre as they will change during crank movement but will remain at the joint of link 2 & 3.      

Step 4. I₁₃ and I₂₄ are secondary I-centre and are located by circle diagram given below.

Fig. 3.13 circle diagram

Take four points 1, 2, 3 and 4 on the circle equal to the number of links in the mechanism. Join these point by solid lines 1-2,2-3,3-4 and 4-1.These lines will be specify the I-centre’s I₁₂,I_23,I₃₄ and I₁₄.Two remaining I-centre’s I₂₄ and I₁₃ are located by joining points 1 to 3 and 2 to 4 showed by dotted lines.

7.3 TYPES OF I-CENTRE

There are basically three types of I-centre Fixed, Permanent, Neither fixed nor permanent 

The fixed I-centre means its location will remain same during the relative motion between the links because one of the links involve is fixed to the ground as I-centres I₁₂ & I₁₄ in the figure 3.12. The permanent I-centres are those whose location will change depending on the position of links but they will remain at permanent joining points of the two links as I-centres I₂₃ & I₃₄ in figure 3.12. The remaining two I-centres I₂₄ & I₁₃ are neither fixed nor permanent types of I-centres as it will change continuously depending on the location of other I-centres. 

Example: 3.2 Slider-crank mechanism has a crank length of 125 mm which is rotating at 600 r.p.m. (clockwise direction). Find the velocity of slider and angular velocity of connecting rod if the length of connecting rod is 500 mm and crank makes an angle of 45⁰ with the inner dead centre.

Solution:

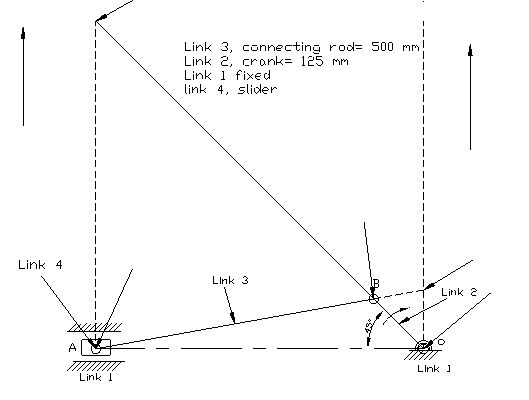
                                      Fig.3.14 slider crank mechanism

Find the number and location of all the I-centers by following the method as describe in above article. Then, Locate the fixed and permanent I-centre I_12,I₃₄ and I ₂₃ by inspection. As slider (link 4) moves in a straight line so I-centre I₁₄ will lie at infinity. Locate remaining two I-centre’s I₂₄ and I₁₃ by using Kennedy theorem.

By measuring from the above diagram we can have

I₁₃A = 581 mm

I₁₃B = 690 mm

Velocity of slider A

\[\omega\times {\text{OB}} = \frac{{{\text{2}}\pi\times {\text{6}}00}}{{{\text{6}}0}}{\text{ = 62}}.{\text{9}}0{\text{rad/s}}\]

\[{{\text{V}}_B}{\text{=}}{\omega _{{\text{OB}}}} \times {\text{OB = 62}}.{\text{9}}0 \times 0.{\text{125 = 7}}.{\text{86 m}}/{\text{s}}\]

\[\frac{{{{\text{V}}_{\text{A}}}}}{{{{\text{I}}_{{\text{13}}}}{\text{A}}}}= \frac{{{{\text{V}}_{\text{B}}}}}{{{{\text{I}}_{{\text{13}}}}{\text{B}}}},{V_A} = 0.{\text{581}} \times {\text{7}}.{\text{86}}/0.{\text{69}} = {\text{6}}.{\text{61m/sec}}\]

 Angular velocity of connecting rod

\[{\omega_{AB}}{\text{=}}\frac{{{{\text{V}}_{\text{A}}}}}{{{{\text{I}}_{{\text{13}}}}{\text{A}}}}= \frac{{{\text{6}}.{\text{61}}}}{{0.{\text{581}}}} = {\text{11}}.{\text{37rad}}/{\text{s}}\]

Example 3.3: Find the linear velocities of the points B, C & D by using I-centre method and also find the angular velocities of the links AB, BC and CD for the diagram shown below.

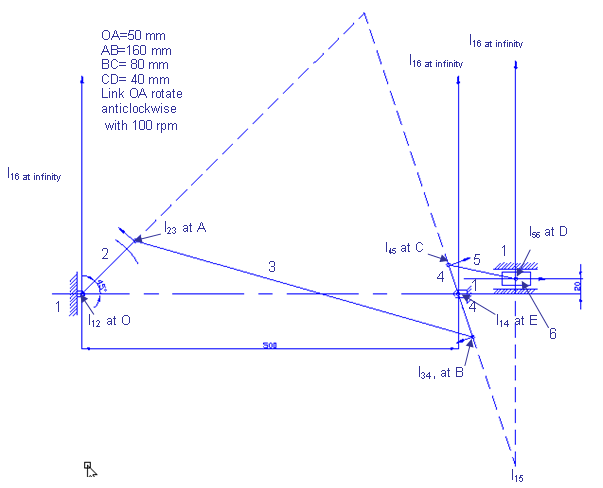
Fig: 3.15

Solution:

Step 1. Write down all the I-center’s in the table        

I12	I23	I34	I45	I56
I13	I24	I35	I46
I14	I25	I36
I15	I26
I16

 

Step 2. Locate all the fixed and permanent I-centre by inspection

                    I₁₂,I_23, I₃₄,I_45, I₅₆,I_16, I₁₄

Step 3. Locate I-centre I₁₅ by using Kennedy theorem as it will be used in finding the slider velocity

Step 4. Locate I₁₃ by Kennedy theorem as it is common I-center of points A and B.

Step 5. find V_A= ω × OA

Step 6. considering I-center I₁₃ because point A and point B rotate about this I-center and have zero velocity at this point. So use

eq. \[\frac{{{V_A}}}{{{I_{13}}A}} = \frac{{{V_B}}}{{{I_{13}}B}}\] and find V_B

Step 7. similarly, considering I-center I₁₄, use eq. \[\frac{{{V_B}}}{{{I_{14}}B}} = \frac{{{V_C}}}{{{I_{14}}C}}\] and find V_C

Step 8. similarly, considering I-center I₁₅, use eq. \[\frac{{{V_C}}}{{{I_{15}}C}} = \frac{{{V_D}}}{{{I_{15}}D}}\] and find V_D

Angular velocity of links AB can be found by using eq. \[{\omega _{AB}} = \frac{{{V_A}}}{{A{I_{13}}}}\]

Similarly find velocities for links BC and CD