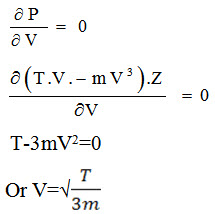Theory of Machines

Lesson 24.

Mathematically the equation is:

\[\frac{{{{\text{N}}_{\text{2}}}{\text{ }}}}{{{{\text{N}}_{\text{1}}}}} = \frac{{{{\text{D}}_{\text{1}}}}}{{{\text{ }}{{\text{D}}_{\text{2}}}}}\] 

N₁ = Speed of driver pulley in rpm

_­ N₂ = Speed of driven pulley in rpm

_­D₁ = Diameter of driver pulley in mm

_­ D₂ = Diameter of driven pulley in mm

When the thickness of the belt (t) is considered, then velocity ratio is given by

\[\frac{{{{\text{N}}_{\text{2}}}}}{{{{\text{N}}_{\text{1}}}}} = {\text{ }}\frac{{\left( {{{\text{D}}_{\text{1}}} + {\text{ t}}} \right){\text{ }}}}{{\left( {{{\text{D}}_{\text{2}}} + {\text{t}}} \right)}}\]

24.2 SLIP OF BELT DRIVES

The forward motion of the driver without carrying the belt with it is called slip of the belt and is generally expressed in percentage. For slippage velocity ratio is given by

\[\frac{{{{\text{N}}_{\text{2}}}}}{{{{\text{N}}_{\text{1}}}}}={\text{}}\frac{{\left({{{\text{D}}_{\text{1}}}+{\text{t}}}\right){\text{}}}}{{\left({{{\text{D}}_{\text{2}}} + {\text{t}}} \right)}}\times {\text{ }}\left( {{\text{1}} - \frac{{\text{S}}}{{100}}} \right)\]

Where S= S₁+S₂ (total percentage of slip)

S₁ = Percentage slip between driver and the belt and

S₂= Percentage slip between belt and the follower

24.3 Length of open belt drive

Consider an open belt drive; both the pulleys rotate in the same direction as shown in the figure 5.7

Let r₁ and r₂ be radii of larger and smaller pulley

    X= distance between the centres of two pulleys i.e. (C₁, C₂)

    L= Total length of the belt

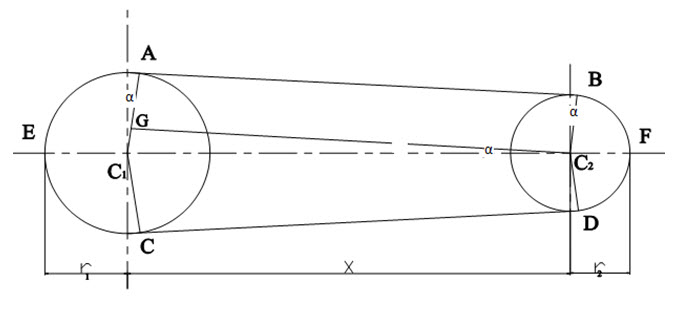
Fig. 5.7 Length of open belt drive

Let the belt leaves the larger pulley at A and C and smaller pulley at B and D. Through C₂ draw C₂G parallel to AB.

From the figure, C₂G will be perpendicular to C₁A.

Let the angle GC₂C₁=α radians

We know that length of belt is given by

L= Arc CEA+AB+Arc BFD+DC

  =2(Arc AE+AB+Arc BF)

From the figure,

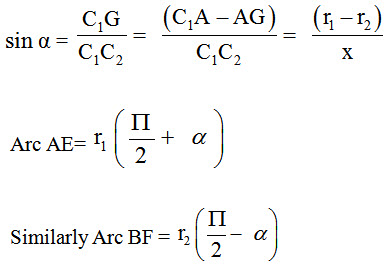
AB= GC₂= [(C₁C₂)² – (C₁G) ²]^1/2= [x²-(r₁-r₂)²]^1/2

Expanding by binomial theorem

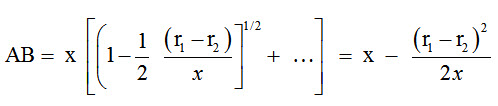
Substituting the values of arc AE from equation, arc BF and AB from equations we get

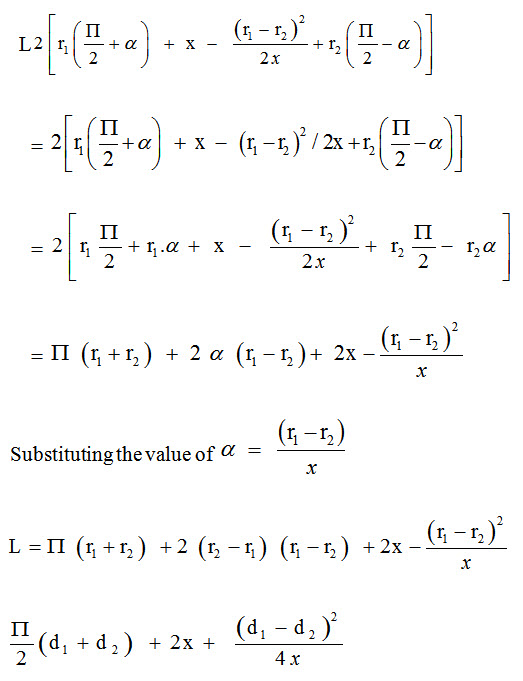
24.4 Ratio between belt tensions

A driven pulley rotating in clockwise direction is shown in figure 5.8

Let T₁ = Tension on tight side of the belt

T₂ = Tension on slack side of the belt

θ = Angle of contact of belt with pulley in radians

µ = Coefficient of friction between the belt and pulley.

Considering a small portion of belt XY in contact with the pulley. X makes angle δθ at the centre of the pulley. Let T be the tension in the belt at X and (T + δT) be the tensions in the belt at Y.

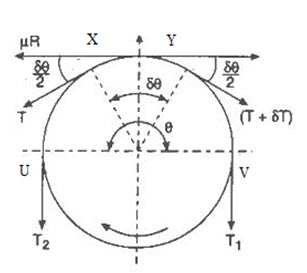
Fig 5.8 Ratio of driving tensions

The belt portion XY is in equilibrium under the action of following forces:

1.    Tension T in belt at X.

2.   Tension T + δT in belt at Y.

3.   Frictional reaction R at U.

4.   Frictional force µR between belt and pulley.

Now again solving the forces expression in horizontal direction

µR = (T + δT) cos (δθ / 2) - T cos (δθ / 2) 

Since δθ is very small

cos (δθ / 2) = 1

µR + T = (T + δT)

µR = δT                                                                                  …(1)

and resolving the force is vertical reaction.

R = T sin (δθ / 2) + (T + δT) sin (δθ/2)

Since, δθ is very small, so

R = T δθ/2 + (T + δT) δθ/2 = T δθ                             …(2)

From equations (1) and (2)

µ(T δθ) = δT                                        (neglecting δT. δθ / 2  )

δT / T = µ δθ

On integration, we get

^T2∫_T1 δT/T = ∫_o^θ µdθ

loge T₁ / T₂ = µθ

T₁ / T₂ = (e)^µθ

24.5 Power transmitted by belt drive

Power transmitted, P = (T₁ - T₂) V    (Watt)

V is the velocity of the belt =  \[ = \frac{{{\text{ }}{{\text{D}}_{\text{1}}}{{\text{N}}_{\text{1}}}}}{{60}}\] (m/sec)

24.6 Tension in the belts

The initial tension (T₀) ensures that the belt would not slip under designed load. Belts are mounted on the pulleys with a certain amount of tension T₀. At rest, the forces acting on the two sides of belts are equal. As the power is transmitted, the tension on the tight side increases and tension on the slack side decreases.

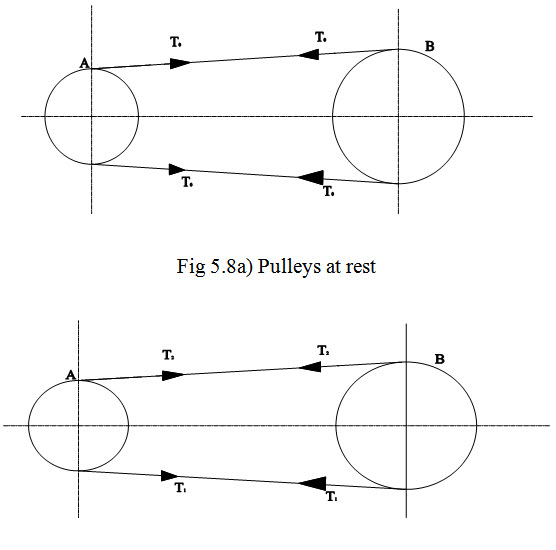 Fig 5.8 (b) Pulleys Working

Mathematically Initial tension is given by

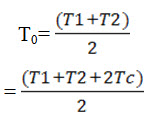
Where T₁ and T₂ are tensions on tight side and slack side and T_c is the centrifugal tension given by

Tc=mv²

Where m= mass of belt per unit length and V=Velocity of belt in m/s

24.7 Condition for the transmission of Maximum power

Power transmitted by belt drive is given by

P= (T₁-T₂) V…………………………….(1)

Where T₁= Tension in the belt on tight side

          T₂= tension in the belt on slack side

    V= velocity of belts

Also \[\frac{{{{\text{T}}_{\text{1}}}}}{{{{\text{T}}_{\text{2}}}}} = {{\text{e}}^\mu }^\theta \]

Substituting the value of T₂, we get

\[= ({{\text{T}}_{\text{1}}}--{\text{ }}\frac{{{{\text{T}}_{\text{1}}}{\text{ }}}}{{{{\text{e}}^{\mu \theta }}}}){\text{V}} = {\text{ }}{{\text{T}}_{\text{1}}}({\text{1}} - \frac{{\text{1}}}{{{{\text{e}}^{\mu \theta }}}}){\text{V}} = {{\text{T}}_{\text{1}}}.{\text{V}}.{\text{Z}}\] ……………… (2)

Where

\[{\text{Z}} = {\text{1}} - \frac{{{\text{1 }}}}{{{{\text{e}}^{\mu \theta }}}}\] 

Also maximum tension (T) in the belt considering centrifugal tension (Tc) is given by

T=T₁+T_c

Substituting the value T₁ in equation (2)

P= (T-T_c) V.Z= (T.V-mV³) Z

Differentiating with respect to V for maximum power and equate to zero