Soil & Water Conservation Structures 3(2+1)

Lesson 9. Open Channel Flow

9.2 Types of Flows in Open Channel

Open channel are classified in to following classes depending on the relative change in the flow regime with respect to time and space.

(a)    Steady Flow and Unsteady Flow

If the flow characteristics do not change over time at any point, the flow is called steady flow whereas if the flow characteristics are changed with time, the flow is called unsteady flow. Mathematically, for steady flow the conditions ∂v/∂t and ∂v/∂x should be equal to zero and vice-versa for unsteady flow.

 (b)    Uniform Flow and Non-Uniform Flow  

The flows are classified under these classes when space is considered as the criteria. When the depth of flow is unchanged over different section of the channel, the flow called as uniform flow. Whereas the depth of flow changes with section, the flow classified as varied flow. Fig 9.1 shows the uniform flow and the varied flow. The varied flow is further classified as rapidly varied flow (RVF) and gradually varied flow (GVF). In case of RVF, the flow changes abruptly over a short distance such as hydraulic jump. In case GVF, the flow changes gradually over the length in a long reach of the channel, such as irrigation canal network.

 

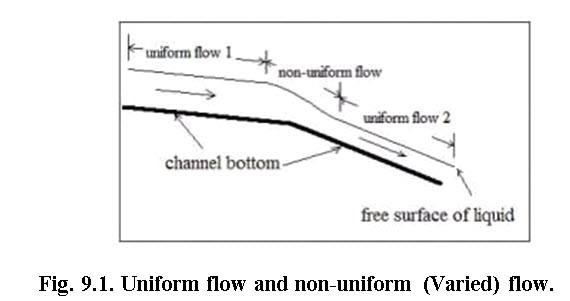
(Source: http://www.engineeringexcelspreadsheets.com/wp-content/uploads/2011/07/uniform-and-nonuniform-flow.jpg)

 The following figure describes the classification of flow in different section of channel. The flow characteristics are changed due to different flow conditions are illustrated in the Fig.9.2.

 

 

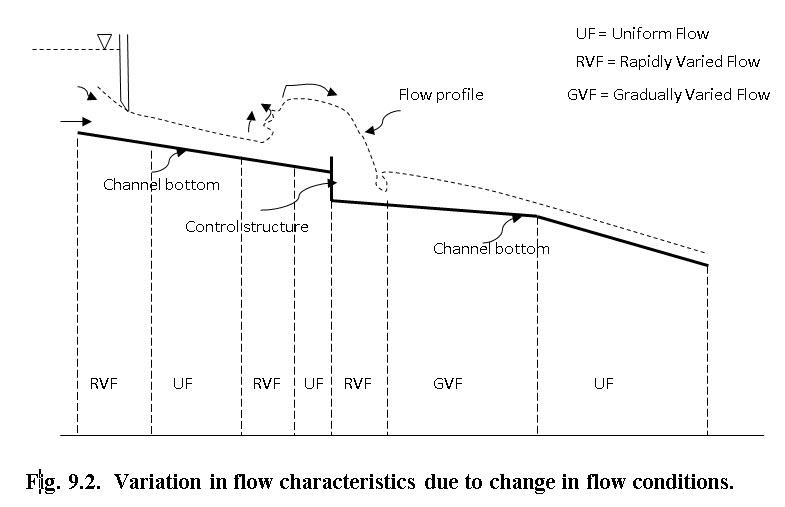
(Source: www.taiwan921.lib.ntu.edu.tw)

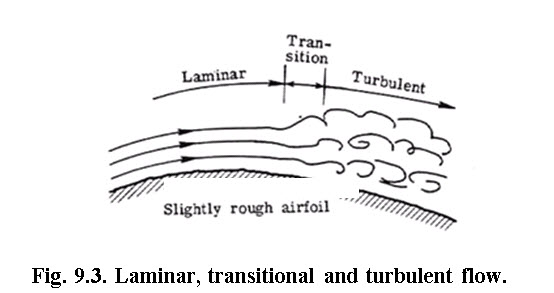
 (c)   Laminar and Turbulent Flow

The Reynolds number (R_e) is used to characterize the flow as laminar, turbulent or in transition state. The Reynolds number is defined as the ratio of viscous force to inertia force. If R_e is less than 500, the flow is laminar, for R_e in between 500 to 2000, the flow is in transitional state and the flow is turbulent if R_e is greater than 2000 (Modi and Seth, 1991).   The reynold number is given as

 

 

Where, is the reynold number,  is mass density of water,  is mean velocity of water  is hydraulic radius and  is absolute viscocity. The hydraulic radius, R, also called as hydraulic mean depth, is the ratio of wetted area to its wetted perimeter.

 (Source: http://www.avalanchecenter.org/Education/topics/wind1.php)

 

In laminar flow the fluid particles will appear to move in definite smooth paths or streamlines. Laminar flow is known to occur in shallow overland or sheet flow conditions. Turbulent flow is the most common type occurring in open channel drainage facilities, it is the type considered for most hydraulic procedures.

 

(d)    Subcritical, Critical and Super Critical Flow

The regimes of flow which may be present in an open channel are subcritical flow, critical flow and supercritical flow. This flow regime which exists under a given set of conditions may be determined by calculation of the Froude Number. The Froud number defines the relative effect of gravity and inertia forces causing water to flow and is expressed as:

 

                                                

  Where  is Froud number, is mean velocity of flow and  is hydraulic depth. Hydraulic depth is defined as the ration of wetted area to the top width.

Subcritical flow :exists when the Froude Number is less than 1.0. Subcritical flow is characterized by low velocities and large depths. When a channel is operating in the subcritical flow regime, the formation of a hydraulic jump is not possible. If the channel cross-section and the discharge are constant, then the regime of flow becomes a function of the slope of the channel. In this case, the slope of the channel defines the flow regime and the slope may be referred to as either subcritical slope, critical slope, or supercritical slope. In order for subcritical flow to occur, the channel slope must also be subcritical. Critical flow will occur when the Froude Number is equal to 1.0. For a given channel cross section and discharge, critical flow will occur when the channel slope is equal to the critical slope.  = velocity distribution coefficient

 Supercritical Flow: Supercritical flow will occur when the Froude Number is greater than 1.0. Supercritical flow is characterized by high velocities and shallow depths. When a channel is operating in the supercritical regime, the formation of a hydraulic jump is possible. A hydraulic jump will occur when the flow regime changes from supercritical to subcritical in a short distance. For example, a hydraulic jump will occur in a channel if the channel slope abruptly changes from a supercritical value to a subcritical value.

References

• Bansal, R. K. (2009). Fluid Mechanics and Hydraulic Machines, Laxmi Publications (P) Ltd, New Delhi, pp. 771-774.

• Das, M. (2008).  Fluid Mechanics and Turbo machines,  Prentice Hall of India Pvt. Ltd., New Delhi, pp. 226.

• Modi, L. P. N. and Seth, S. M. (1991). Hydraulics and Fluid Mechanics, Standard Book House, Delhi 6.

• Office of Design. (2009).  Drainage Handbook Open Channel. Drainage Section Tallahassee, Florida.

 Internet References

• http://freeit.free.fr/The%20Civil%20Engineering%20Handbook,2003/0958%20ch30.pdf

• http://en.wikipedia.org/wiki/Open-channel_flow

• http://www.efm.leeds.ac.uk/CIVE/CIVE2400/OpenChannelHydraulics2.pdf

• http://ebookbrowse.com/seventheory-pdf-d232506679

Suggested Readings

• Bansal, R. K. (2009). Fluid Mechanics and Hydraulic Machines, Laxmi

• Publications (P) Ltd, New Delhi, pp. 771-774.

• Modi, L. P. N. and Seth, S. M. (1991). Hydraulics and Fluid Mechanics, Standard Book House, Delhi 6.

• Subramanya, K. (1991). Flow in Open Channels, Tata McGraw-Hill New Delhi.

• http://www.efm.leeds.ac.uk/CIVE/CIVE2400/OpenChannelHydraulics2.pdf

• http://ebookbrowse.com/seventheory-pdf-d232506679