Site pages
Current course
Participants
General
Module 1. Perspective on Soil and Water Conservation
Module 2. Pre-requisites for Soil and Water Conse...
Module 3. Design of Permanent Gully Control Struct...
Module 4. Water Storage Structures
Module 5. Trenching and Diversion Structures
Module 6. Cost Estimation
Lesson 11. Energy and Momentum
The total energy head at a point in an open channel is the sum of the potential and kinetic energy of the flowing water. The potential energy is represented by the elevation of the water surface i.e., the sum of depth of flow (h) and the elevation of channel bottom (z) from an arbitrary datum. The water surface elevation is a measure of the potential work that the flow can do during its movement from a higher elevation to a lower elevation. The kinetic energy is the energy of motion as measured by the velocity (v).
As water flows down a channel, the flow loses energy because of friction and turbulence. The total energy head between two points in a channel reach can be set equal to one another if the losses between the sections are added to the downstream total energy head. This equality is commonly known as the energy equation, as described in lesson 10 (equation 10.7) which is expressed as:
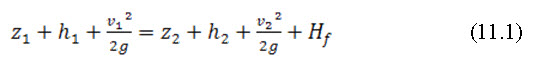
Where, andare channel elevations above an arbitrary datum at channel sections 1 and 2, respectively;andare depth of open channel flow at channel sections 1 and 2, respectively; and are average channel velocities at channel sections 1 and 2, respectively; is the head or energy loss between channel sections 1 and 2 and is the acceleration due to gravity.
Now, as described in lesson 10, according to Newton's Second Law of Motion, the change of momentum per unit of time is equal to the resultant of all external forces applied to the moving body.
11.1 Specific Energy
The total energy of a flowing liquid per unit weight is given by,

Where, z is the height of the bottom of the channel from datum; his the depth of liquid; v is the mean velocity of flow
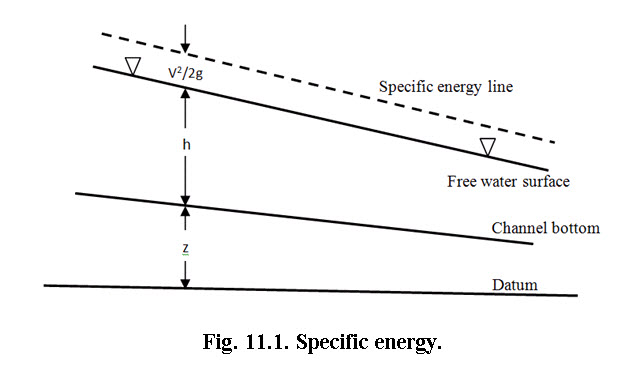
Fig. 11.1. Specific energy.
Consider the channel bottom as the datum, and then the total energy per unit weight of liquid will be,

Eq. (11.3) gives the specific energy of a flowing liquid. Therefore, the specific energy of a flowing liquid is the energy per unit weight of the liquid with respect to the bottom of the channel
11.2 Specific Energy Curve
It is the curve which shows the variation of specific energy with depth of flow. Specific energy curve is obtained as,
From eq. (11.3) Specific energy of a flowing liquid,
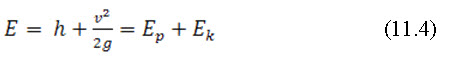
Where,EP is the potential energy of flow (h) and Ek is the kinetic energy of flow (v2/2g).
Now, consider a rectangular channel with a steady but non-uniform flow. Let Q is the discharge through the channel, b is the channel width, h is the depth of flow and q is the discharge per unit width i.e. Q/b

Substituting the value of v in eq. (11.3), we get;
![]()
Eq. (11.6) gives the variation of specific energy (E) with the depth of flow (h). Hence, for a given discharge Q, for different values of depth of flow, the corresponding values of E may be obtained. Then a graph between specific energy, E (along X-X axis) and depth of flow, h (along Y-Y axis) may be plotted.
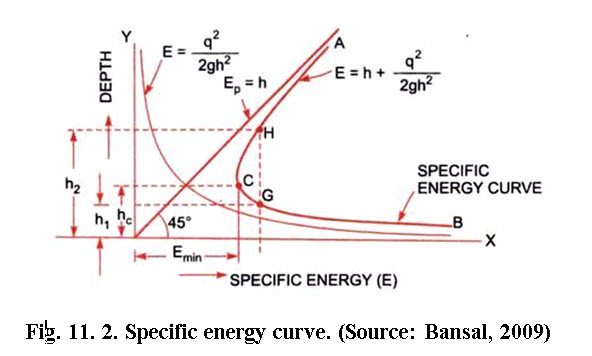
11.3 Critical Depth
Critical depth (hc) is defined as the depth of flow of water at which the specific energy is minimum. In figure 11. 2, curve ACB is a specific energy curve and point C corresponds to the minimum specific energy. The depth of flow of water at C is known as critical depth. The mathematical expression for critical depth is obtained by differentiating the specific energy equation (11.6) with respect to depth of flow and equating the same to zero.
or 
Where,
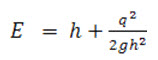 From eq. (11.6)
From eq. (11.6)
or 
But when specific energy is minimum, depth of flow is known as critical depth. Hence, critical depth is

11.4 Minimum Specific Energy in Terms of Critical Depth
From eq. (11.6), specific energy of a flowing fluid is given by,

However, at critical depth the value of specific energy of a flowing fluid is minimum. Hence, the above eq. (11.10) for critical depth of flow can be written as,

From eq. (11.8) we have,
or 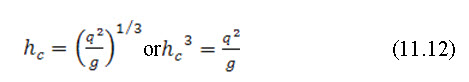
Substituting the value of in eq. (11.11), we get

11.5 Specific Force
Specific force may be explained from the momentum equation discussed in the Lesson-10 which is as follows;
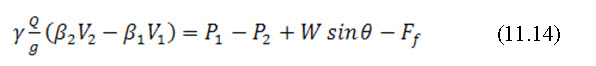
Where, p1 ansd p2 are the resultants of pressure acting on two sections (i.e. hydrostatic forces); W is the weight of water enclosed between section 1 and 2;Ff is the total external force of friction and resistant action along the surface of contact between the water and the channel; b1and b2 are the momentum coefficient at section 1 and 2; Y is the unit weight of water; Q is the discharge; V1 and V2 is the mean velocity of flow at section 1 and 2;
If the channel is short, horizontal and prismatic, Ff and are neglected and
![]()
Now, the momentum equation can be simply written as:

the hydrostatic pressure forces P1 and P2 are respectively,
and 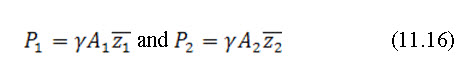
Where, ![]() and are the distances to the centroid below the surface of the flow at section 1 and 2.
and are the distances to the centroid below the surface of the flow at section 1 and 2.
Also, 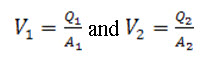
Then the momentum equation reduces to
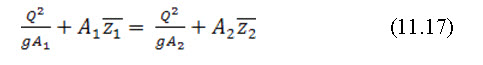
The two sides of the above equation are analogous and hence may be reduced to a general form for a short channel section as;

The first term of the above equation represent rate of change of momentum of the flow passing through the channel section per unit weight of water and the second term is the force per unit weight of water.
Since both terms are essentially force per unit weight of water, their sum is known as the specific force and equation (11.18) is known as specific force equation
11.6 Hydraulic Jump and its Application
When the depth of flow changes rapidly from a low stage to a high stage, it results in an abrupt rise of water surface. This local phenomenon is known as ‘hydraulic jump’. It frequently occurs in a canal below a regulating sluice, at the toe of a spillway, at downstream of narrow channel or at the place where a steep channel slope suddenly turns flat. (For hydraulic jump see lesson-12)
Hydraulic jump has many practical applications. It is used,
1) To dissipate the high kinetic energy of water near the toe of the spillway and to protect the bed and banks of a river near a hydraulic structure.
2) To raise water level for irrigation and other distribution works.
3) To increase the discharge of a sluice by holding back tail water.
4) To mix of chemicals in water purification plant.
5) To remove air pockets from water supply lines and prevents air locks.
6) To aerate the stream polluted by bio-degradable materials.
Solved Examples:
Problem 11.1: For a discharge of 10 cumec through a rectangular channel of 5 m width what will be the specific energy of the flowing water if the depth of water in the channel is 3m.
Solution:
Width of the channel, b = 5 m; Discharge, Q = 10 cumec; Depth of water, h = 3 m.
Hence, 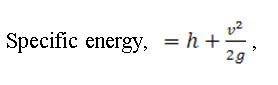
Where,

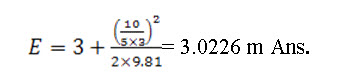 = 3.0226 m Ans.
= 3.0226 m Ans.
Problem 11.2: What would be the critical depth of the water flowing through a rectangular channel of 4 m width, when discharge is 16 m3/s.
Solution:

From eq. (11.9) Critical depth is given by,
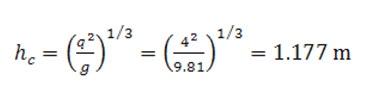 Ans.
Ans.
Problem 11.3: A rectangular channel carries a discharge of 18 m3/s and the width of the channel is 6 m. Find the minimum specific energy of the flowing water.
Solution:
Minimum specific energy at critical depth. Hence, first we will calculate the value of critical depth.
Discharge per unit width,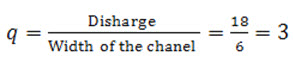 cumec/m
cumec/m
From eq. (11.9) Critical depth is given by,

Now from eq. (11.13) The value of minimum specific energy,
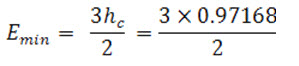
= 1.4575 m of water Ans.
Reference
Bansal, R. K. (2009). Fluid Mechanics and Hydraulic Machines, Laxmi Publications (P) Ltd, New Delhi, pp. 771-774.
Das, M. (2008). Fluid Mechanics and Turbomachines, Prentice Hall of India Pvt. Ltd., New Delhi, pp. 226.
Das, M.( 2008). Open Channel Flow, Prentice Hall of India Pvt. Ltd., New Delhi, pp. 191-192.
Internet References
-
http://nptel.iitm.ac.in/courses/IIT-MADRAS/Hydraulics/pdfs/Unit9/9_1.pdf
-
http://nptel.iitm.ac.in/courses/IIT-MADRAS/Hydraulics/pdfs/Unit28/28_1.pdf
-
http://www.dot.state.fl.us/rddesign/dr/files/OpenChannelHB-11-09.pdf
Suggested Readings
-
Bansal, R. K. (2009). Fluid Mechanics and Hydraulic Machines, Laxmi Publications (P) Ltd, New Delhi, pp. 771-774.
-
Das, M. (2008). Fluid Mechanics and Turbo machines, Prentice Hall of India Pvt. Ltd., New Delhi, pp. 226
-
http://www.efm.leeds.ac.uk/CIVE/CIVE2400/OpenChannelHydraulics2.pdf
-
http://mysite.du.edu/~etuttle/tech/opench.htm#Spec
-
http://filebox.vt.edu/users/moglen/ocf/index.html
-
http://www.dot.state.fl.us/rddesign/dr/files/OpenChannelHB-11-09.pdf