Soil & Water Conservation Structures 3(2+1)

Lesson 22. Design of Chute Spillway

22.1 Design Layout of Chute Spillway

The structural details of straight inlet, straight channel and SAF type outlet are presented in Fig. 22.1.

 

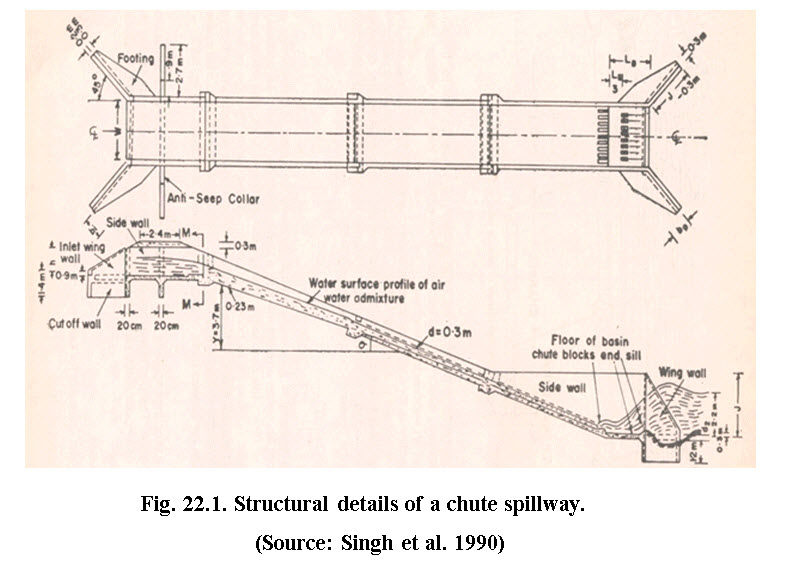
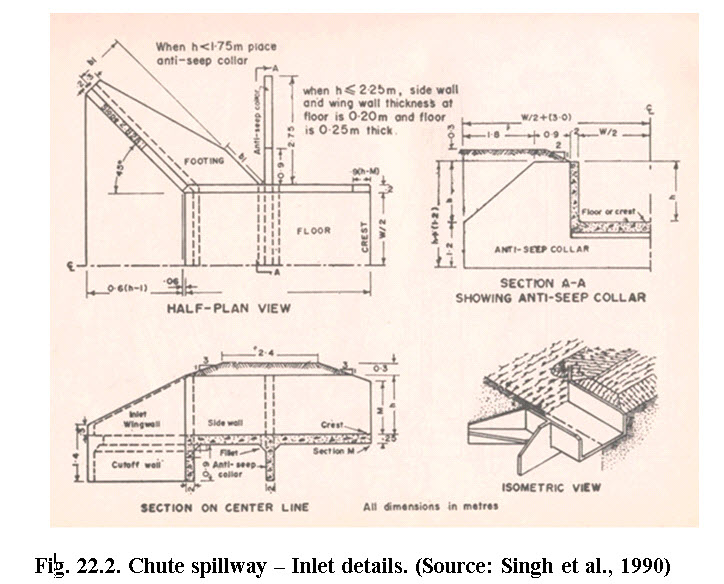
Figs. 22.2 and 22.3 present the inlet and channel details of chute spillway. The design procedure for inlet is more or less similar to that of drop structures except design of stilling basin and tail water. The channel is designed in such a way that the flow remains sub-critical.

 

22.2 SAF Stilling Basin Design

The Saint Anthony Falls (SAF) stilling basin, shown in Fig. 22.4, provides chute blocks, baffle blocks, and an end sill that allows the basin to be shorter than a free hydraulic jump basin. It is recommended for use at small structures such as spillways, outlet works, and canals where the Froude number at the dissipater entrance is between 1.7 and 17. The reduction in basin length achieved through the use of appurtenances is about 80 percent of the free hydraulic jump length. The SAF stilling basin provides an economical method of dissipating energy and preventing stream bed erosion.

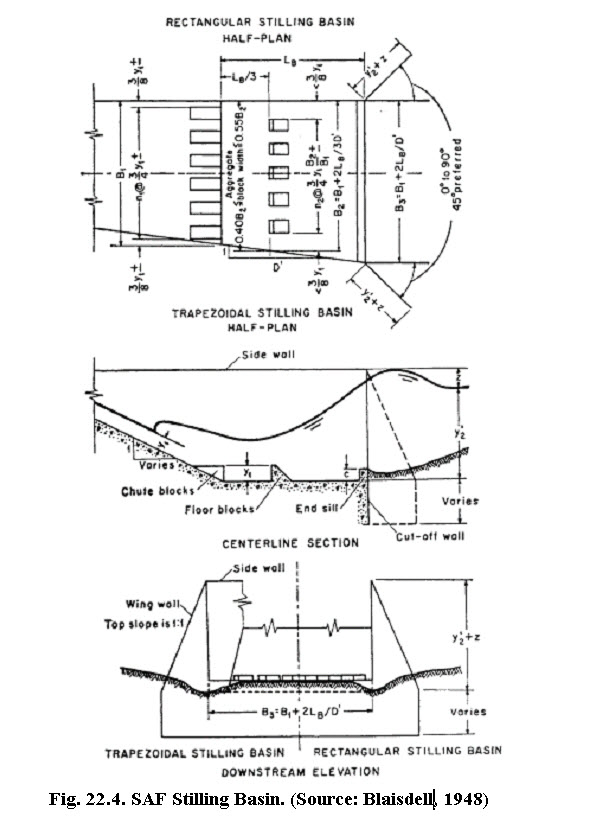
Referring Fig. 22.4, the dimensions of different components of SAF stilling basin are given under (Blaisdell, 1948):

1. Length of stilling basin (L_B) is given by

 This equation is valid for the Froud number ranging between 1.7 to 17. The Froud number can be calculated by the equation, F₁ =, in which y₁ represents the height of chutes and floor blocks.

2. Width and spacing of the chutes as well as floor blocks = 0.75y₁
3. Distance from the upstream end of the stilling basin to the floor block = 
4. No floor blocks should be place closer tothe side walls than  y₁.
5. The floor blocks should be placed at downstream side from the openings between the chute blocks.
6. The height of the end sill should be equal to 0.07 y₂,
7. The actual depth of tail water above the stilling basin can be computed by the equation,

            for F₁= 1.7 to 5.5                (22.2a)

                             for F₁= 5.5 to 11.0              (22.2b)

                for F₁= 11 to 17                  (22.2c)

 8.The height of the side wall above the maximum tail water depth is given by                       

                                

 9.Height of wing wall should be equal to the height of stilling basin’s side wall.

10.The top of wing wall should have a slope of 1:1.

11. The wing wall may be placed at an angle of 45⁰ to the centre line of the outlet.

12. The width of stilling basin at the downstream end (B₃) is given by

 

        

 

In which, D' is the slope of flare given to the side wall and B₁ = basin width at upstream equal to chute channel width.

13.  In order to make structure safe against sliding, a cutoff wall of nominal depth should be provided at the end of stilling basin.

14.  In the design of stilling basin the effect of entrained air should be neglected.

 22.3 Structural Design

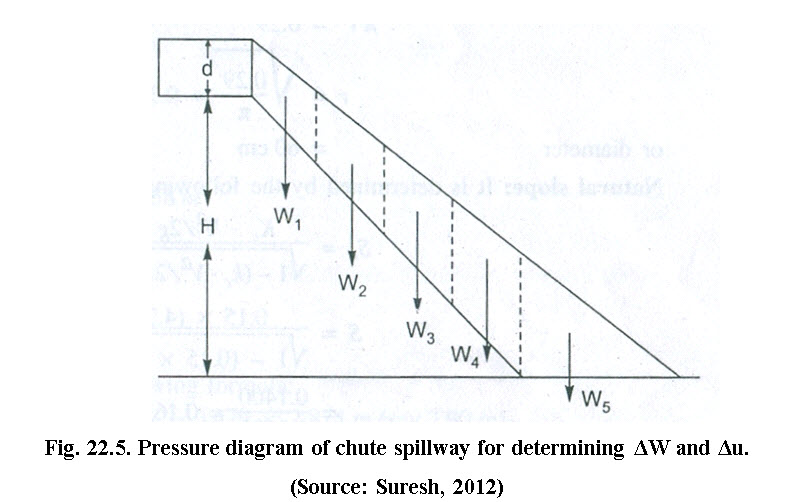
Structural design of chute spillway deals with the determination of the thickness of stable chute floor. The thickness of floor is initially assumed to check the stability at every section. The structure is considered to be stable, when the weight of the structure (ΔW) is greater than the uplift pressure due to water (Δu) (i.e. ΔW > Δ u). The uplift pressure over the structure is calculated by drawing the pressure diagram.  The pressure is assumed equal to the depth of flow and zero at the beginning of the structure and at the outlet end, respectively. The pressure diagram is then divided into a number of equal parts and area of each part is calculated. The uplift pressure is obtained by multiplying the density of water with area of pressure diagram. The detail is shown in Fig. 22.5.

Example 22.1:

Design a chute spillway for a gully head with a drop of 3.5 m, laid on a 1.5:1 slope. The slope of flare given to the side wall is 1.5:1. The width of the gully is 4.5 m and the catchment area is 25 ha. From the records, it has been found that the maximum intensity of rainfall based on a 50 – year recurrence interval is 10cm / h, for the duration equal to the time of concentration. The runoff coefficient for the rational formula is 0.35. The spillway is to have a straight inlet with a depth of flow of 0.70 m, and a SAF stilling basin at the outlet.

Solution:

The peak flow rate for the design of the structure is determined by using the Rational formula:

                                               

Inlet width

The spillway is to be provided with straight inlet, therefore, the flow discharge through it is

                                     

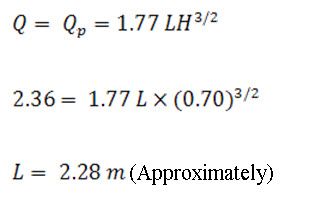
              Flow velocity at the stilling basin toe is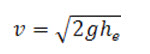

           

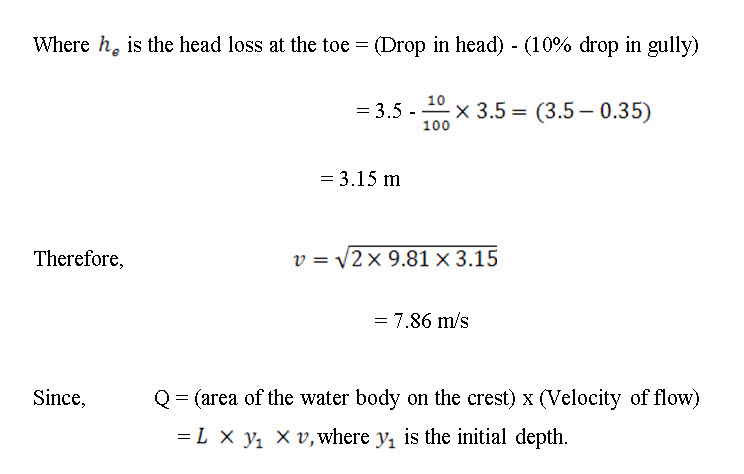
       Therefore, the initial depth of flow,

                              

 

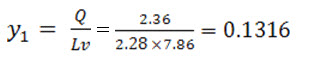
Froud number,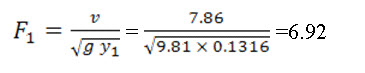      

 Sequent depth y₂, the depth of water after hydraulic jump is determined by the following formula;

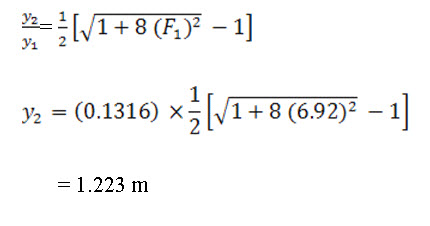
 Design Dimensions

1. Floor and chute blocks height = y₁ = 0.1316 m
2. Spacing and width between floor and chute blocks = 0.75y₁

                                                              = 0.75 x 0.1316 = 0.0987 m

 3.  Distance (minimum) of the floor blocks from the side walls = 0.375 x

                                                                             = 0.375 x 0.1316

                                                                                = 0.05 m

4. Tail water depth over the stilling basin,

                            y'₂=0.85y_2=0.85 x 1.223 =1.039 m

5. Stilling basin length = LB = 1.265 m

6. Side wall and stilling basin height = 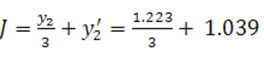 = 1.44 m

7. Transverse sill height = 0.07 x y₂= 0.07 x 1.223 = 0.0856 m

8. Side wall freeboard to be provided above the tail-water depth =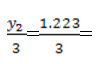 0.41 m

9. Wing wall height = stilling basin side wall height = 1.44 m

10. Width of stilling basin

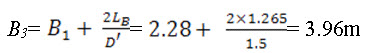
 Structural Design

The weight of the structure should be more than the uplift force. Assume a rectangular channel section, and make thickness of the material 15 cm. The details of the structure pressure diagram shown in Fig. 22.6. The uplift pressure head on the channel of the chute is divided into four sections. Since the channel slope is 1.5:1, therefore, the total horizontal width of the sloping channel section is 5.25 m. Dividing it into 4 equal sections, the water body in each section will have a horizontal width of 1.3125 m.

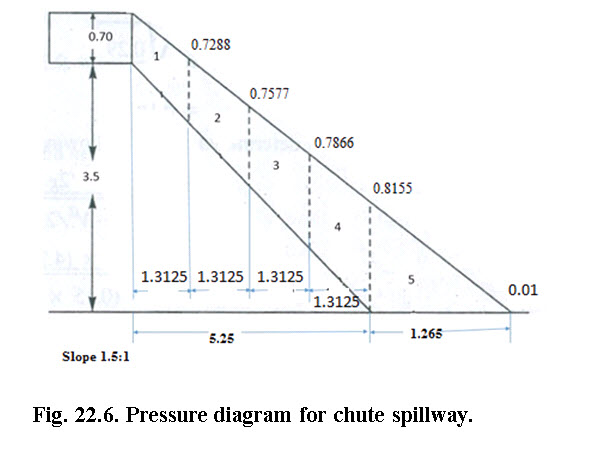The head at these sections are calculated as under, for example, the head in the first case is

 

       

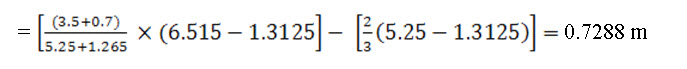
 Similarly, the values of the heads for rest of the sections are calculated (see Fig. 22.6).

 The area of water in each section which will have the shape of a trapezium,

 

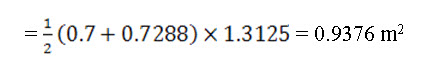
Therefore the uplift force in the first section = water area × width of the channel × density of water

 

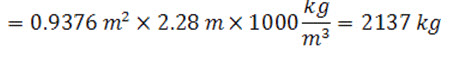
The length of total channel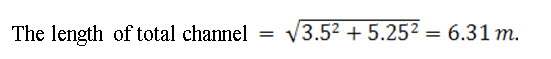

Length of each section = 6.31/4 = 1.577 m.

Width of channel section = 2.28 m.

 The weight of the section of the structure

 = Cross-sectional area of the section x thickness of concrete x density of concrete =1.577 x 2.28 x 0.15 x 2300 = 1240 kg

Weight of the two sides of the wall on each section = 2(1.577×1.44×0.15×2300)

=1567 kg

Total weight of each section = (1567+1240) = 2807 kg

 Weight of the Stilling Basin

Weight of the base = L_B x B₃ x Thickness X Density of concrete

Weight of the base = 1.265 x 3.96 x 0.15 x 2300 =1728 kg

The height of the side walls of the stilling basin = 1.44 m

Weight of the side walls = (1.265×1.44×0.15×2300) ×2 = 1257 kg

Total weight of the stilling basin = 1728 +1257 = 2985 kg

 The computations pertaining to each section and the associated structure stability are all shown in a tabulated form.

 Table 22.2. Cumulative value for each section

Section no.	Head of each section upstream (m)	Head of each section downstream (m)	Horizontal width of the water body (m)	Each section area (m2)	Uplift force (kg)	Cumulative uplift force (kg) Δ u	Weight of each section (kg)	Cumulative weight of structure (kg)  ΔW	Stability of structure
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
1.	0.7	0.7288	2.28	0.93765	2137.84	2137.842	2807	2807	Safe
2.	0.7288	0.757751	2.28	0.975549	2224.25	4362.094	2807	5614	Safe
3.	0.757751	0.786627	2.28	1.013498	2310.77	6672.871	2807	8421	Safe
4.	0.786627	0.815503	2.28	1.051398	2397.18	9070.057	2807	11228	Safe
5.	0.815503	0.01	3.96	0.52213	2067.63	11137.69	2985	14213	Safe

 

Therefore the structure designed is safe.

References

• Chanson, H. (2002). Hydraulics of Stepped Chutes and Spillway, Taylor and

• Francis Publication, pp 199-284.

• Das, G. (2000). Hydrology and Soil Conservation Engineering, Prentice-Hall

• India, pp 356-377

• Hydraulic Design of Energy Dissipaters for Culverts and Channels. (2000). Hydraulic Engineering, Circular no.14, Third edition.

• Singh, G, Venkataramanan, C., Sastry, G.,  and Joshi, B. P. (1990). Manual of Soil and Water Conservation Practices. CSWCR&TI, Dehradun.

• Suresh, R. (1993). Soil and Water Conservation Engineering, Standard Publishers Distributors, New Delhi, pp 190-243

Suggested readings

• Blaisdell, F. W. and Mortaz, A. F. (1961). Soil and Water Conservation- Erosion Control Structures, Agricultural Engineering Handbook, McGraw-Hill, New York

• Blaisdell, F.W., The SAF stilling basin, Agricultural Handbook, No., 156, USDA., 1948

• USDA, SCS Engineering. Handbook, sec. 14, Oct 28, 1985.

• http://www.fhwa.dot.gov/engineering/hydraulics/pubs/06086/hec14.pdf