Heat and Mass Transfer 2(2+0)

Lesson 1. Heat Transfer, Importance of Heat Transfer, modes of Heat Transfer

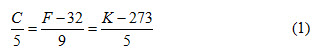
Heat: Heat is a form of energy which is transient in nature and it flows from one point to another point. When two bodies of different temperatures come in contact with each other, the two temperatures approach each other and after some time become equal. This equalization of temperature of the bodies is on account of flow of energy in the form of heat from one body to another. Therefore, heat may be defined as flow of energy from one body to another body by virtue of temperature difference between them. The net flow of energy always occurs from high temperature body towards low temperature body and this flow of heat stops the moment temperature of both the bodies are equal. Thus, flow of heat is a non-mechanical transfer of energy occurring due to a temperature difference between two bodies. 

  According to the international system of units (S.I.), the unit of measurement of heat is Joule.

  1 Joule = 1 Newton meter

               = Watt-second

 1 kcal = 4.182 Χ 10³ Joule

  1 kWh = 3600 kJ

 Heat Transfer and Thermodynamics:

Thermodynamics and heat transfer are related to each other. The laws of thermodynamics form the basis of science of heat transfer. However, there are few fundamental differences between thermodynamics and heat transfer which are given in Table 1.1:

Table 1 : Fundamental Differences in Thermodynamics and Heat Transfer

1.	Thermodynamics is a science which deals with equilibrium states and the changes from one state to another during a process.	Heat transfer is a non-equilibrium phenomenon as it occurs when thermal equilibrium is disturbed.
2	Thermodynamics is a science which deals with amount of heat transferred during a process.	Heat transfer is a science that deals with the rate as well as mode of heat transfer during a process.
3.	Thermodynamics is a science which deals with amount of work done during a process.	Heat transfer indicates the temperature distribution inside a body.

 Modes of Heat Transfer:

Heat transfer is the study of transmission of thermal energy from a high temperature region / body to a low temperature region / body on account of temperature difference. The rate of heat transfer is directly proportional to the temperature difference between the heat exchanging regions / bodies. Once the process of heat energy is complete, it is stored in one or more forms of energy such as potential, kinetic and internal energy.  It is pertinent to mention that energy in transition as heat can never be measured; however, it is determined in terms of observed changes in other forms of energy. Transfer of heat between two regions / bodies maintained at different temperatures can occur in three different modes namely:

• Conduction

• Convection

• Radiation

In the conduction and convection modes, heat flows from high temperature to low temperature region / body whereas in radiation mode, transfer of heat takes place from both the bodies towards each other. However, net transfer of heat is always from high temperature body to low temperature body. Mechanism of heat transfer in each mode is different and controlled by different laws.

Conduction:

Conduction is a process of heat transfer from a high temperature region to a low temperature region with in a body or between different bodies which are in direct physical contact. In heat conduction, energy is transferred due to exchange of molecular kinetic energy. According to kinetic theory, temperature of body is proportional to the mean kinetic energy of its constituent molecules. As the temperature in one region of a body increases, kinetic energy of molecules in that region also increases as compared to that of the molecules of adjacent low temperature region. High energy molecules transfer a part of their energy by impact in case of fluids or by diffusion in case of metals to low energy molecules, thereby resulting in increase in their energy levels, hence temperature. Likewise, this process of energy transfer by molecular activity continues till temperature along the entire length of the body becomes equal and has been depicted in Figure 1.

Heat transfer by conduction in solids, liquids and gases is determined by the thermal conductivity and temperature difference. The basic law of heat transfer by conduction was proposed by the French Scientist J. B. J. Fourier in 1822 and one dimensional Conduction rate equation described by the Fourier Law is written as:

   Where,  Q_x - Heat Flow, (W)

       k – Thermal conductivity of the material, ( W/(m-K)

       A – Cross-sectional area in the direction of heat flow, (m²)

      dT/dx – Temperature gradient, (K/m)

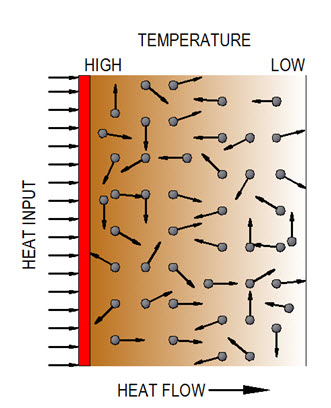
Figure 1

Convection:

Heat transfer by convection occurs when a fluid (Liquid and gas) comes in contact with a solid through direct contact and a temperature difference exists between them. Heat transfer by Convection occurs under the combined action of heat conduction and mixing motion.

When a fluid comes in contact with a hot surface, energy in form of heat flows by conduction from hot surface to the adjacent stagnant layer of fluid particles, thereby increasing their temperature and internal energy. Due to increase in temperature, density of the fluid particles decreases and they become lighter as compared to the surrounding fluid particles. The lighter fluid particles move up to a region of lower temperature with in the fluid where they mix and exchange a part of their energy with colder fluid particles. Simultaneously, the cold fluid particles move downwards to occupy the space vacated by hot fluid particles. This upward and downward movement of hot and cold fluid particles continues till temperature of the fluid and the surface becomes equal. The convection heat transfer process has been shown in Figure 2.

The upwards movement of hot fluid particles and downward movement of cold fluid particles is called convectional currents. If the convectional currents are set up only due to density differences, then the heat transfer process is termed as natural or free convection.

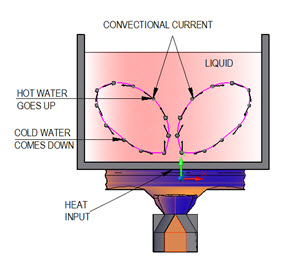
Figure 2                      

However, if the convectional currents are caused by some external means such as blower, fan, pump etc. then heat transfer process is called forced convection.

It is virtually impossible to observe pure heat conduction in a fluid because as soon as a temperature difference is imposed in a fluid, natural convection currents will occur due to resulting density differences.

Convective heat transfer rate is governed by Newton’s law of cooling and is expressed as

                             Q = h A_s (T_s – T_f)                                                                          (3)

Where, ‘h’ is convective heat transfer coefficient in W/ (m² – K)

             A_s is heat transferring area, m²

             T_s and T_f are temperatures of surface and the fluid respectively, K               

Radiation:        

Heat exchanged between two bodies or mediums, which are separated and are not in contact with each other, is called radiation heat transfer. Radiation heat transfer does not require presence of an intervening medium between the two bodies as in case of conduction and convection and it takes place most effectively in a vacuum. Example of radiation heat transfer is the energy received on the earth from the Sun and has been shown in Figure 3.

Thermal radiation is the energy emitted by a body in the form of electromagnetic waves due to changes in the electronic configuration of the constituent atoms or molecules of the body. The electromagnetic waves travel through the intervening medium between two bodies with a speed that is related to speed of light in vacuum by the following equation

c= c_o / n.                                                                                    (4)

Where c is the speed of propagation in a medium,

C_o is the speed of light in vacuum and is equal to 3 X 10⁸ m/sec,

 ‘n’ is an index of refraction of a medium which is unity for air and most of the gases, 1.5 for glass and 1.33 for water.

When electromagnetic waves come in contact with a body, energy is transferred to the body as thermal energy which is partly absorbed, reflected and transmitted.

Energy emitted per unit area as thermal radiation is called emissive power of a body and the maximum energy emitted as radiation by a body at a particular temperature is governed by Stefan-Boltzmann law which is expressed as

E_b = σ AT⁴                                                             (5)

Where, E_b is the energy emitted per unit time, W

                  A is the surface area, m²

                  T is the absolute temperature of the body, K

                  σ is Stefan-Boltzmann constant which is equal to 5.67 Χ 10 ^-8 W/(m² – K⁴)

At a given temperature, maximum radiations are emitted by an ideal emitter called black body. The energy emitted by non-black bodies are less as compared to that of the ideal body when both the bodies are maintained at same temperature. Energy emitted by a non-black body maintained at temperature ‘T’  is given as

E = ε σ AT⁴                                                                (6)

Where, ε is called emissivity of non-black bodyand is defined as ratio of emissive power of a non- black body to that of a black body. Emissivity is a radiative property of the body and its value depends upon surface characteristics and temperature of the body.

All the bodies radiate energy and receive energy emitted by other bodies simultaneously. Consider heat exchange between two black bodies maintained at temperatures T₁ and T₂   respectively and body 1 is completely enclosed by body 2. The net heat transfer by radiation from body 1 to body 2 is given as

Q_1-2 = σ A₁(T₁⁴ – T₂⁴)                                                   (7)

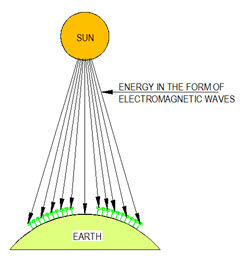
Figure 3

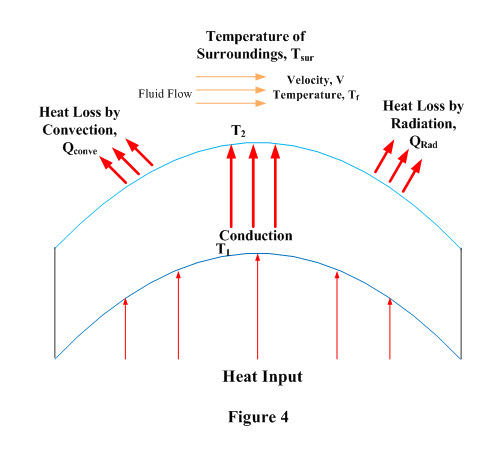
Surface Energy Balance:

Consider a cylinderical object of thickness ‘L’ which is being heated from inside and is surrounded by a fluid at temperature ‘T_f’ and moving at a velocity ‘V’. Heat is being transferred from inner surface to outer surface by conduction and conducted heat is transferred to surroundings by radiation and convection and has been depicted in Figure 4.

The energy balance equation for the arrangement can be expressed as

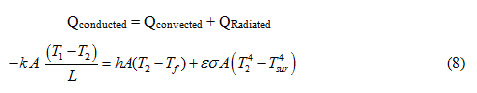
Q. 1.1 Two surfaces of a plane wall of 15cm thickness and 5 m² area are maintained at 240°C and 90°C respectively. Determine the heat transfer between the surfaces and temperature gradient across the wall if conductivity of the wall material is18.5 W/(m-K).

Solution:         Given : T₁= 2 40°C, T₂= 90°C,  Thickness of wall, x = 15 cms.=0.15 m,

                                         Area, A= 5 m², Thermal conducivity, k=18.5 W/(m-K)

                          To determine: i) Temperature gradient,  ,

                                                ii) Heat transfer rate, ,  

i) The temperature gradient in the direction of heat flow is

(b) Heat flow across the wall is given by Fourier’s heat conduction equation

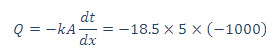
=92500 W or 92.50 kW

Example 1.2   The bond between two plates, 2.5 cm and 15 cm thick, heat is uniformly applied through the thinner plate by a radiant heat source. The bonding epoxy must be held at 320 K for a short time. When the heat source is adjusted to have a steady value of 43.5 kW/m² , a thermocouple installed on the side of the thinner plate next to source indicates a temperature of 345 K. Calculate the temperature gradient for heat conduction through thinner plate and thermal conductivity of its material.

Solution:         t₁ = 345 K  ;   t₂ = 320 K

                        δ = 2.5 cm = 0.025m

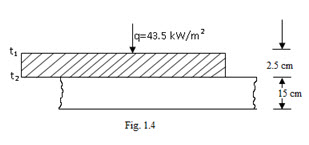
Temperature gradient,

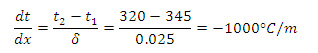
Example 1.3   A 120 W system is used to maintain a plate of 0.2m² area at a temperature of 60° C when the surroundings are at 30°C temperature. What fraction of heat supplied is lost by natural convection? It may be presumed that convection coefficient conforms to the relation h = 2.5 (ΔT)^0.2 W/m^{2 K.}

Solution:         Convective heat transfer coefficient,                                  

Heat lost by convection = h A Δt

                                       = 4.9360.2 (60-30) = 29.616 W

Heat lost by convection as fraction of heat supplied,

The remaining 75.32% would be lost to the surroundings by ration.

Example 1.4   A cylindrical system,1 m long and 3 cm in diameter, is heated and positioned in a vacuum furnace which has interior walls at 900 K temperature.Current is passed through the rod and its surface is maintained at 1000K. Calculate the power supplied to the heating rod if its surface has an emissivity of 0.8.

Solution:         For steady state conditions, the electric power supplied to the rod equals the radiant heat loss from it. Further, since the walls of the furnace completely enclose the heating rod, all the radiant energy emitted by the surface of the rod is intercepted by the furnace walls. Thus

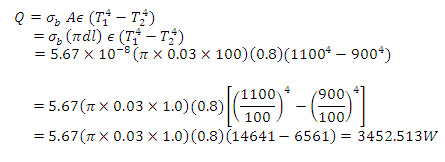
Thus the rate of electrical input to the rod must equal 3452.513 W.

Example 1.5   A surface at 300°C loses heat both by convection and radiation to the surroundings at 150°C. The convection coefficient is 75 W/m²K and the radiation factor due to geometric location and emissivity is 0.85. If the heat is conducted to the surface through a solid material of thermal conductivity 15 W/mK, determine the temperature gradient at the surface of the solid.          

 

Solution:         Under steady state conditions,

                        Heat convected + heat radiated = heat conducted

            Given: T₁=300+273=573 K and T₂=150+273=423 K

            Considering unit area and substituting the appropriate values, we obtain

           

            Or

            11250+3652.43=

                        Thus, the temperature gradient at the surface of solid is