Heat and Mass Transfer 2(2+0)

Lesson 7. Numericals on conduction

Value of thermal conductivity of a material is generally used as a measure of its insulating capabilities. Materials having lower value of thermal conductivity are considered to be insulators. Insulating capability of a material depends upon following factors

• Thermal conductivity

• Temperature

• Density or Porosity

• Specific heat

• Surface emissivity

• Moisture Content

• Air Pressure

• Convection with in insulating material

According to ‘Thermal Insulation Association of Canada’ thermal insulation is used for temperature range of -75 ^oC and 815 ^oC as for temperature range below -75 ^oC and higher than 815 ^oC, cryogenic and refractory materials are used respectively. Depending upon temperature range for which thermal insulation is to be used, insulating materials are categorized as

i)              Low temperature insulating materials for temperature range of -75 ^oC to 15 ^oC

ii)            Medium temperature insulating materials for temperature range of 15 ^oC to 315 ^oC

iii)          High temperature insulting materials for temperature range of 315 ^oC to 815 ^oC

The most commonly used insulating materials and their properties are given in Table 1

TABLE 1– Thermal Conductivities of Insulating Materials (Powders)

	Material	Mean Temperature  °C	Conductivity (K) k cal/ m-hr-°C
1.	Alumina compressed powder	50	7.0
2.	Ashes, Soft wood	25	0.33
3.	Carbon black	55	0.22
4.	Coal dust	40 100	1.20 1.32
5.	Coke dust	25	1.50
6.	Charcoal	15	0.54
7.	Cork-granulated	0	0 45
8.	Floto foam	35	0.30
9.	Graphite powder	40	1.40
10.	Plaster of Paris	25	10.5
11.	Fine river sand Moistured	10	3.3
12.	Saw dust	25	11.6
13.	Silica	30	0.06
14.	Silica Aerogel	315 480 650	0.80 0.84 0.93
15.	Silica gel	-70 -20 40 100 150 55	0.174 0.207 0.240 0.276 0.318 0.90
16.	Snow	0	0.51 to 1.9

 

Critical Thickness of Insulation

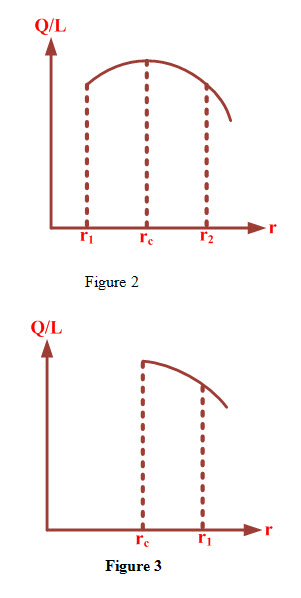
Addition of layer insulation to walls and slabs always reduces the heat transfer, however, in case of systems having cylindrical and spherical surfaces, addition of insulation does not reduce the heat transfer, rather it increases heat transfer rate upto certain thickness of insulation. As insulation layer is added to a bare pipe, heat transfer rate increases instead of decreasing.  With further addition insulation layer, heat transfer rate goes on increasing till it attains a maximum value beyond which it decreases with increase in thickness of insulation material. The thickness of insulation corresponding to maximum heat transfer rate from the pipe is called critical thickness of insulation.

This concept of critical thickness of insulation finds a useful application in electric transmission cables. Transmission losses increase with increase in temperature as electric current passes through the cables. In order to reduce the transmission losses, it becomes imperative to increase heat transfer rate from cables to surroundings so that temperature of cables is reduced. This is achieved by keeping the thickness of insulation equal to its critical thickness.

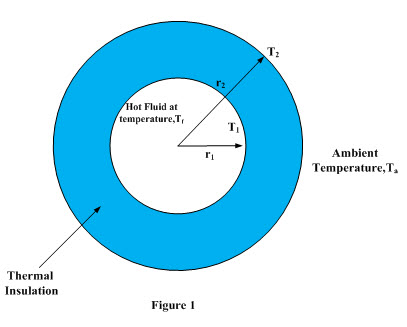
In order to determine the critical thickness of insulation, consider a cylinder of negligible thickness, length ‘L’, radius ‘r₁’ carrying hot fluid of temperature T₁. Temperature of hot fluid is higher than that of ambient temperature T_a. The cylinder is insulated by an insulating material having thickness‘t’ and thermal conductivity ‘k’. Thickness of insulation can be expressed as

 t = r2 – r1                                                         (1)

where r₂ is the outer radius of the arrangement consisting of thin cylinder and layer of insulating material and it depends upon value of the  thickness of insulating material. The arrangement has been shown in Figure 1.

Heat transfer rate per unit length from cylinder is expressed as

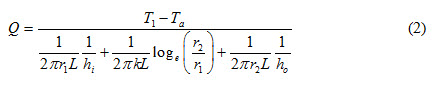
h_i and h_o inside and outside heat transfer coefficients of convection

By using equation (1), heat transfer rate per unit length can be determined for different value of r₂. Total thermal resistance of the arrangement is sum of inside convective thermal resistance, conductive thermal resistance of insulating material and outside convective thermal resistance. Total thermal resistance of the arrangement depends upon the value of r₂ which in turn depends upon the thickness of insulating material. As the thickness of insulation increase, r₂ also increase resulting in increase in conductive thermal resistance and decrease in outer convective resistance. Therefore, increase in thickness of insulation will either result in increase or decrease in heat transfer rate depending on the overall change in the total thermal resistance.

For heat transfer rate per unit length to be maximum, thermal resistance should be the minimum. The value of r_2, for which heat transfer rate per unit length will be maximum, can be obtained by differentiating total thermal resistance i.e. denominator of equation (2) with respect to r₂ and equating equal to zero.

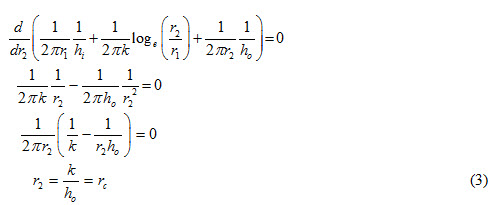
Equation (3) gives the value of thickness of insulation for which heat transfer rate per unit length is the maximum as corresponding total thermal resistance is the minimum. The value of thickness of insulation at which total thermal resistance is minimum is called critical thickness of insulation and is represented by r_c and depends upon thermal conductivity and convective heat transfer coefficient of insulating material. Addition of insulation to a bare surface will either increase or decrease the heat transfer rate per unit lenth depending upon the value of critical radius and radius of bare surface.

i)        If r₁ < r_c , the  rate of heat transfer per unit length of cylinder increases as thickness of insulation increases. The heat transfer rate goes on increasing with increase in thickness of insulation and attains a maximum value corresponding to that value of insulation of thickness for which r₂  becomes equal to r_c as shown in Figure 2 . It is due to the fact that in ranger r₁ less than r_c, progressive decreases in convective resistance with increase in insulation thickness dominates over the corresponding increase in conductive resistance. The net effect is decreases in total thermal resistance and heat transfer rate per unit length increases.

ii)      For the range r₁ greater r_c, heat transfer rate goes on decreasing with increase in insulation thickness as shown in Figure 3. It is attributed to the fact that in range r₁ greater than r_c, effect of conductive resistance dominates over that of the convective resistance resulting in increases in total thermal resistance. Therefore, heat transfer rate per unit length decreases.