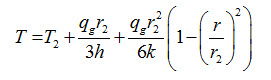Heat and Mass Transfer 2(2+0)

Lesson 4. One dimensional steady state conduction through plane and composite walls, tubes and spheres with heat generation

1)      One-Dimensional Heat Flow through a slab with Heat Generation:

i) When Temperature of Both Sides of Slab is Same:

Consider a slab of thickness ‘L’ and cross-sectional area ‘A’ through which heat flow takes place in x-direction. A heat source located at the center of the slab is generating ‘q_g’ amount of heat per unit volume per unit time as shown in Figure 1.                                                                                      

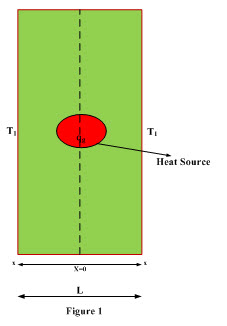
Heat generated is conducted equally towards the sides of the slab through a distance ‘x’ measured from center of the slab along x-direction. Temperature of both sides of the slab is same and is equal to T₁ as same amount of heat is flowing from the center towards the sides of the slab.

At the center of the slab x=0 and at the sides of the slab x= L/2. The general conduction equation under the given conditions reduces to

Integrating equation (1) with respect to ‘x’, we get

Integrating equation (2) again with respect to ‘x’, we get

Using the boundary conditions,

   At x = 0,  , From equation (2), we get

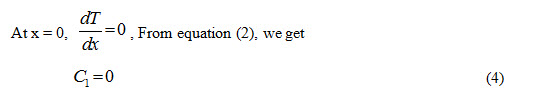
At x = L/2, T = T₁, From equation (3), we get

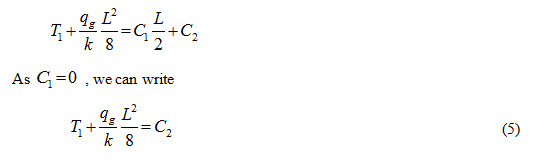
Substituting the values of  and  in equation (3), we get

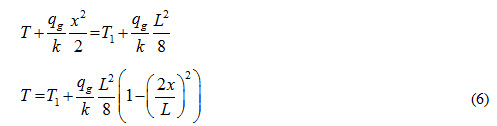
Equation (6) represents temperature distribution equation in the slab having a heat generating source present inside it.

Temperature will be maximum at the center of the slab where x = 0

Flow of heat can be expressed as:

Using equation (2), we can write

  

Substituting value of 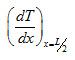   from equation (9) in equation (8), we get    

Equation (10) represents flow from one of sides of the slab; therefore, total heat flow from both the sides is expressed as

Total Heat Conducted form both sides of the slab = Volume x Heat generating capacity

Total Heat Conducted from both sides of the slab = Total Heat generated

Under steady state conditions, heat conducted at x = L/2 must be equal to convected from a side to the atmospheric air. Therefore,

Substituting the value of T₁ from equation (11) in equation (6), we get

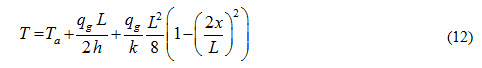
Equation (12) represents temperature distribution. If one side of the slab is insulated

At one side, temperature distribution will be represented by equation (6) except that L/2 will be replaced by L and is expressed as

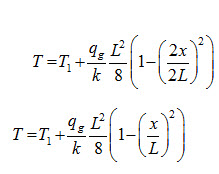
ii) When Temperature of Both Sides of Slab are Different:

If the heat source present inside the slab generates heat q_g per unit volume and heat distribution in towards both slabs is not uniform then the temperature of both sides of the slab will be different as shown in Figure 2.

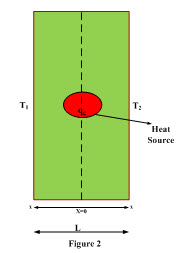
The differential equation governing the heat flow through the slab is expressed as:

Integrating equation (13) with respect to ‘x’, we get

Integrating equation (4.14) again with respect to ‘x’, we get

Applying the boundary conditions,

   At x = 0, T = T₁, From equation (15), we get

C₂ = T₁                                                                        (16)

At x = L, T = T₂,  From equation (15), we get

                                                                        

Substituting the values of  and  in equation (15), we get

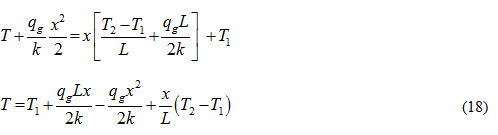
     Subtracting T₂ from both sides of the equation (18), we get

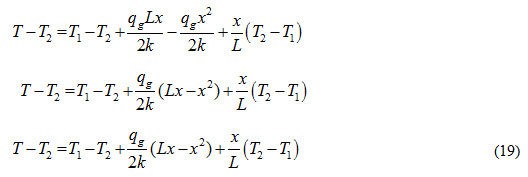
Dividing both sides of the equation (19) with T₁-T₂, we get

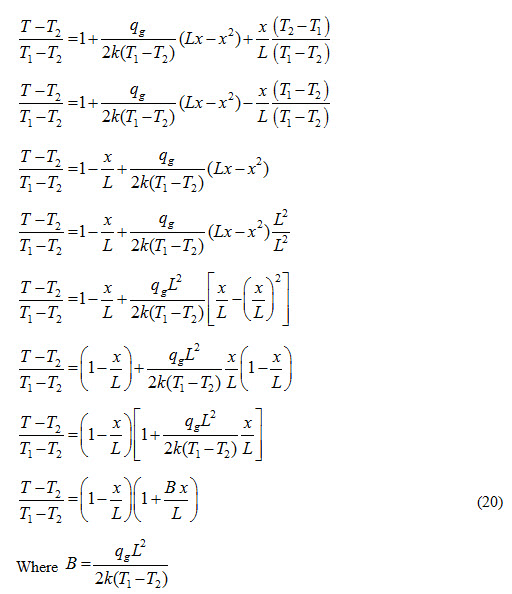
Equation (20) represents temperature distribution equation in the slab having a heat generating source present inside it. In order to find out the location of maximum temperature in the slab equation (20) is differentiated with respect to ‘x’ and equated equal to zero.

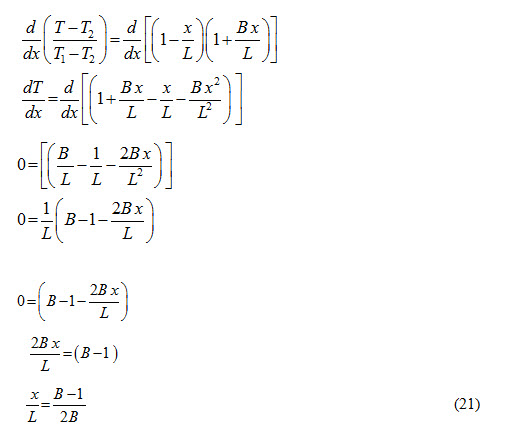
Equation (21) gives the location of maximum temperature in the slab. The equation representing the maximum value of temperature is obtained by substituting the value of maximum x /L from equation (21) into equation (20).

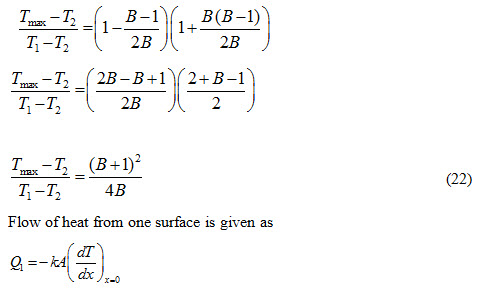
Flow of heat from one surface is given as

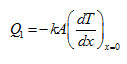
From equation (14) substituting the value of dT/dx, we get

 

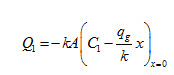
Substituting the value of C₁ from equation (17), we get

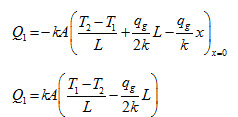
Similarly heat flow from the other surface

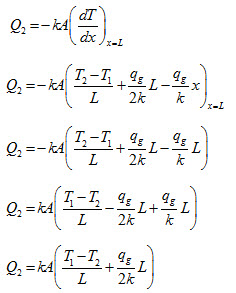
In case maximum temperature occurs inside the slab, heat will flow from both surfaces of the slab and total heat flow will be given as:

  Q_T = Q₁+Q₂

In case T₁ is the maximum temperature, heat will flow towards x (+ve only) and heat lost will be given as:

Q_T = Q₂

One-Dimensional Heat Flow through a cylinder with Heat Generation

i) A hollow Cylinder:

Consider a hollow cylinder of length L having inner and outer radii r₁ and r₂ respectively in which flow of heat is unidirectional along the radial direction. T₁ and T_2­ are temperatures of the inner and outer surfaces of the cylinder respectively. In order to determine temperature distribution and heat flow rate, a small element at radius r and thickness dr is considered. A heat source present inside the strip is generating q_g amount of heat per unit volume as shown in Figure 3.  

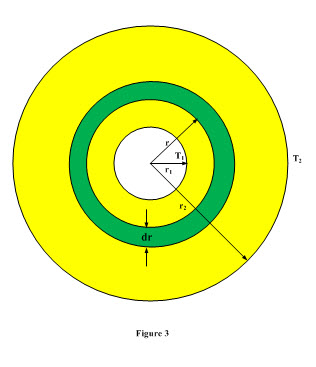
Heat conducted into the element, Q_r = -k(2 Π r L) dT/dr                   (23)                    

Heat generated in the element, Q_g =  2 Π r L dr q_g                                (24)

Heat conducted out of the element,

For steady state condition of heat flow

Heat conducted into the element + Heat generated in the element = Heat conducted out of the element

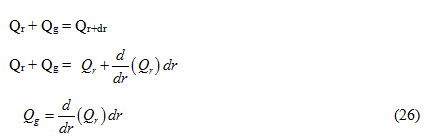
Substituting the values of Q_r and Q_g from equations (23 and 24) in equation (26), we get

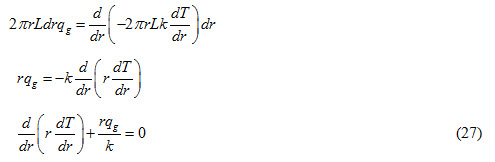
 In order to find out the solution of the above equation, integrate it with respect to r

Integrating equation (4.28) again with respect to r, we get

C₁ and C₂ are constants of integration and the expressions for these constants can be found out by using the following boundary conditions

At r=r₁, T=T₁ and at r=r₂, T=T₂

Subtracting equation (32) from equation (31), we get

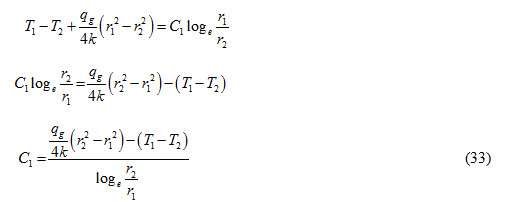
Substituting the value of C₁ in equation (31), we get

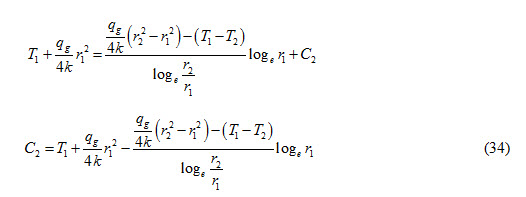
Substituting the values of C₁ and C₂ in equation (30), we get

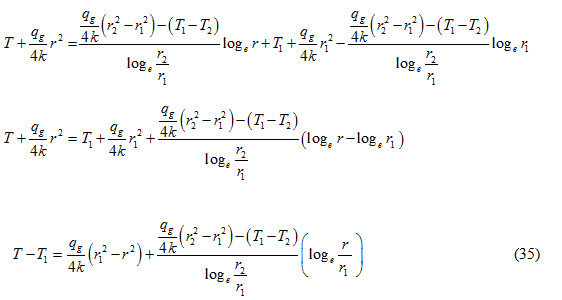
Dividing both sides of equation (35) by T₁-T₂, we get

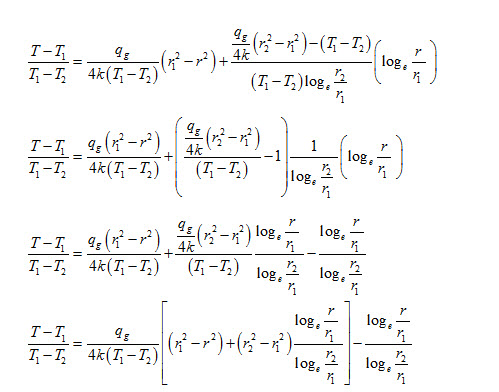
Multiplying and diving Right Hand Side of the above equation by r², we get

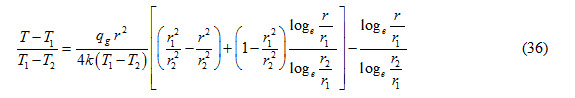
Equation (36) represents temperature distribution inside a hollow cylinder with heat generation.

ii) A Solid Cylinder

In case of solid cylinder, the governing equation remains same as equation (30)

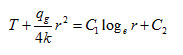
Differentiating above equation with respect to r, we get

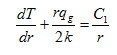
Applying the boundary conditions

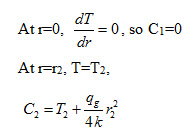
Substituting the values of C₁ and C₂ in equation (30), we get

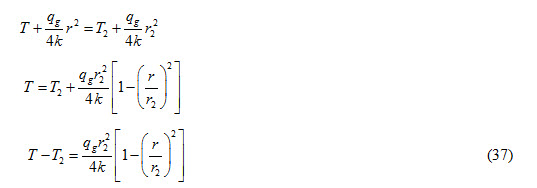
Equation (37) represents temperature distribution equation in a solid cylinder with heat generation. Maximum temperature will occur at r=r₂, and will be expressed as

Dividing equation (37) by equation (38), we get

Heat flow through a solid cylinder is expressed as

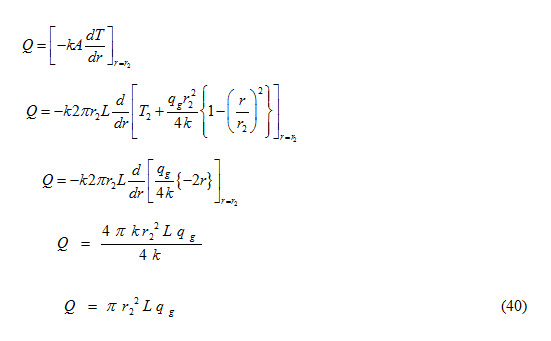
Heat conducted = Volume of cylinder x heat generating capacity per unit volume per unit Time

For steady state conditions, heat conducted at r = r₂ must be equal to heat convected from outer surface of cylinder to the surrounding fluid.

Heat Conducted = Heat convected

From equation (40), we can write

T_f  is temperature of fluid surrounding the cylinder.

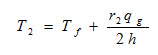
Substituting the value of T₂ in equation (37), we get

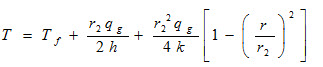
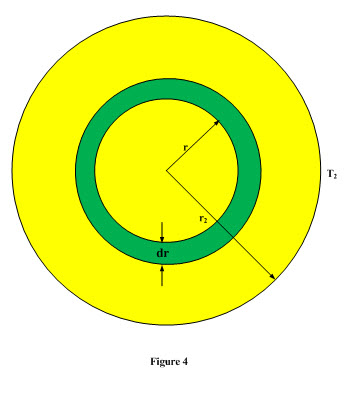
One-Dimensional Heat Flow through a sphere with Heat Generation

Consider steady state heat conduction through a hollow sphere having r₁ and r₂ as inner and outer radii respectively. Temperature of the inner and outer surfaces is T₁ and T₂ respectively. Heat is flowing from inner to outer surface as T₁ is greater than T₂ as shown in Figure 4.

The general conduction equation which governs the conduction heat transfer is written as

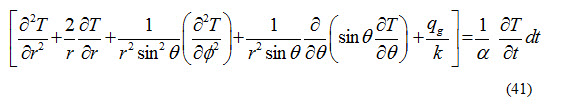
Since it is a case of one-dimensional, stead heat conduction through a wall of uniform conductivity with heat generation, therefore,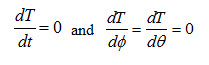

Therefore, equation (41) reduces to

The above equation can be written as

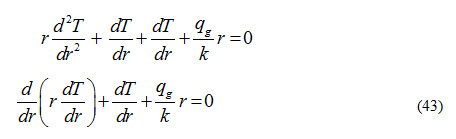
Integrating equation (43) with respect to r, we get

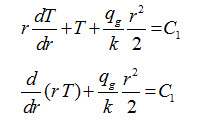
Upon integrating above equation once more with respect to r, we get

Applying the first boundary condition i.e. at  r = 0, dT/dr = 0  to equation (44), we get

C₂ = 0                                                                                     (45)

Applying the second boundary condition i.e  at r = r₂, T =T₂ to equation (43), we get

Substituting the values of C₁ and C₂ in equation (44), we get

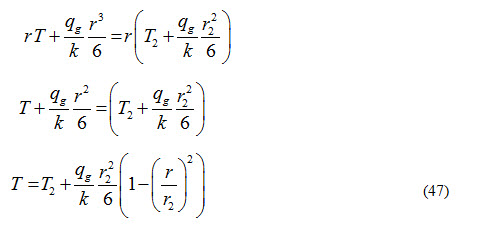
Equation (47) represents temperature distribution equation in a solid sphere having a heat source present inside it.

Heat flow rate through a sphere with heat generation can be determined by using the following equation

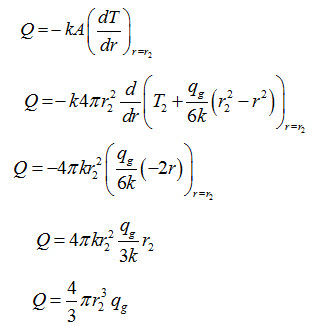
Heat conducted = Volume of sphere x heat generating capacity

For steady state conditions, heat conducted through a sphere must be equal to heat convected from outer surface of the sphere

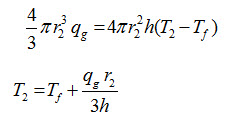
Substitute the value of T₂ from above equation in equation (47), we get