Site pages
Current course
Participants
General
Module 1. Basic Concepts, Conductive Heat Transfer...
Module 2. Convection
Module 3. Radiation
Module 4. Heat Exchangers
Module 5. Mass Transfer
Lesson 5. Electrical analogy and Numerical Problems related to conduction
Electrical Analogy For Conduction Problems
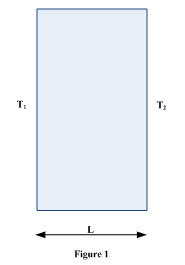
Consider heat flowing through a slab of thickness ‘L’ and area “A’ and T1 and T2 are the temperatures on the two faces of the slab as shown in Figure 1. Heat transfer from high temperature side to low temperature side is expressed as
![]()
Where (T1 –T2) is the thermal potential
![]() is the thermal resistance
is the thermal resistance
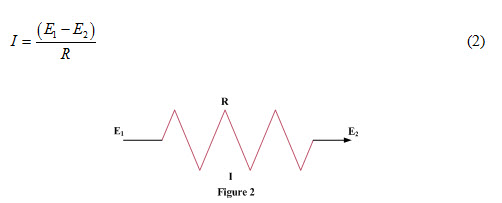
Now, consider an electric circuit having resistance ‘R’ and electric potential E1 and E2 at the ends as shown in Figure 2. Current ‘I’ passing through the circuit can be expressed as
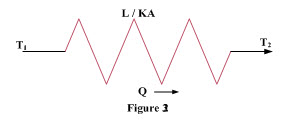
Equations (1) and (2) are found to be symmetrical on comparison. ‘Q’ amount of heat flows through the slab having thermal resistance when a thermal potential (T1 –T2) exits. Similarly, ‘I’ amount of current passes through the circuit having resistance ‘R’ when an electric potential (E1 – E2) exists. Therefore, flow of heat through the slab can be represented by an electric circuit as shown in Figure 3.
If a hot gas at temperature Tg is in contact with one side of the slab and air at temperature Ta at the other side, then heat transfer from the hot gas to air through this slab of thickness can be represented by an electric circuit as shown in Figure 4
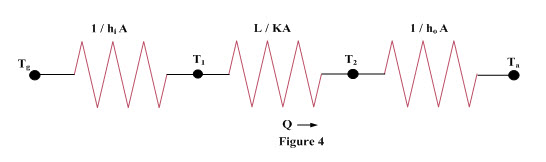
Heat transfer from hot gas to air can be expressed as

For a slab made of three material having thermal conductivities KA, KB and KC respectively and is exposed to a hot gas on one side and atmospheric air on the other side as shown in Figure 5, an equivalent electric circuit has been shown in Figure 6. Heat transfer from the hot gas to atmospheric air is expressed as
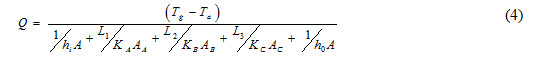

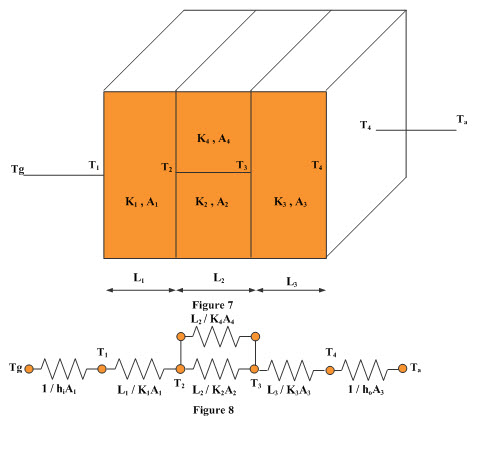
Similarly for the composite slab shown in Figure 7, an equivalent electric circuit has been shown in Figure 8.
Example 3.14 The walls of heating unit in cold region comprise three layers
10cm outer brick work (k =0.75 W/m-deg)
1.5cm inner wooden paneling (k =0.75 W/m-deg)
8cm intermediate layer of insulating material
The insulation layer is stated to offer resistance twice the thermal resistance of brick work. If the inside and outside temperatures of the composite wall are 30°C and -10°C respectively, determine the rate of heat loss per unit area of the wall and the thermal conductivity of the insulating material.
Solution: Thermal resistance for a plane wall of thickness δ, area A and thermal conductivity k is prescribed by the relation Rt =δ/kA

Example 3.15 A furnace wall is a made up of steel plate 10 mm thick (k=62.8 kj/m-hr-deg) lined on inside with silica briks 150 mm thick (k =7.32 kj/m-hr-deg) and on the outside with magnesia bricks 200 mm thick (k = 18.84 kj/m-hr-deg). The inside and outside surfaces of the wall are at temperature 650° C respectively. Make calculations for the heat loss from unit area of the wall.
It is required that the heat loss be reduced to 10Mj/hour by means of air gap between steel and magnesia bricks. Estimate the necessary width of air gap if thermal conductivity for is 0.126 kj/m-hr-deg.
Solution: Thermal resistance for a plane wall of thickness δ, area A and thermal conductivity k is prescribed by the relation Rt =δ/kA.

Example 3.16 A furnace wall comprises three layers: 13.5 cm thick inside layer of fire brick, 7.5 cm thick middle layer of insulating brick and 11.5 cm thick outside layer of red brick. The furnace operates at 870°C and it is anticipated that the outside of this composite wall can be maintained at 40°C by the circulation of air. Assuming close bonding of layers at their interfaces, find the rate of heat loss from the furnace and the wall interface temperature. The wall measures 5m2m and the data on thermal conductivities is:
Fire brick k1 = 2.4 W/m-deg
Insulating brick k2 = 0.14 W/m-deg
Red brick k3 = 0.85 W/m-deg
Solution: The wall area (5m 2m) = 10 m2 is constant for all layers of the composite wall. The thermal resistance Rt of a slab (thickness δ, conductivity k and area A ) is given by

