Heat and Mass Transfer 2(2+0)

Lesson 9. Types of Fins, Fin Applications, Heat Transfer through Fin of uniform cross-section

Using the above two equations, following special cases are considered for heat transfer through a fin of uniform cross section:

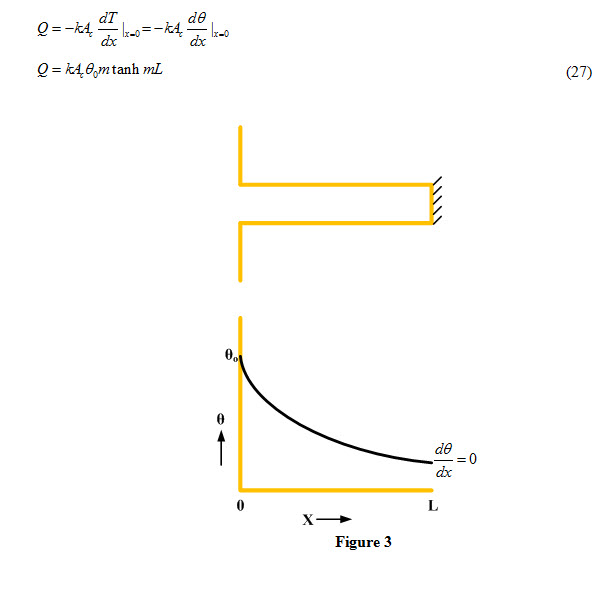
 1. Fin is losing heat at the tip only

When a fin of finite length loses heat only at its tip as shown in Figure 1, the relevant boundary conditions are

i) At the base of fin, its temperature is equal to the wall temperature. Therefore,

At  x = 0; T = T₀

T - T_a = T₀ - T_a

or  θ = θ₀                                                               (3)  

θ₀ represents temperature difference between the fin base and the fluid surrounding the fin.

Applying first boundary condition to equation (2), we get

θ_o­ = c₁  cosh m Χ 0 + c₂ sinh m Χ 0                              

C₁ =  θ_o                                                                                                                                                     (4)                                    

ii) As fin is losing heat at tip only, it means heat conducted through fin is lost to surrounding fluid by convection at tip. Therefore,

                    At  x = L;       

Heat conducted through fin = Heat convected to surrounding fluid by convection  

  

Substituting the value of C₁ from equation (4) in equation (2), we get

θ =  θ_o cosh mx + c₂ sinh mx                                                                            (6)

Differentiating equation (6) with respect to x, we get

Substituting value of   from equation (6) in equation (5), we get   

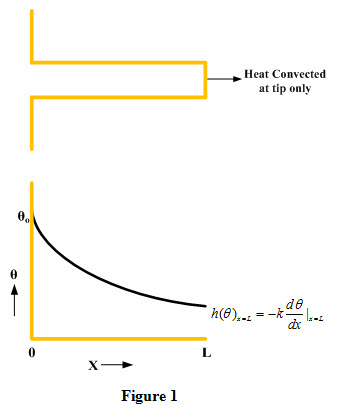
2. Fin is sufficiently long or infinite                                                                                                                                       

For a fin of infinite length as shown in Figure 2, the relevant boundary conditions are:

i) At the base of fin, its temperature is equal to the wall temperature. Therefore,

At  x = 0; T = T₀

T - T_a = T₀ - T_a

or  θ = θ₀                                                                     (16)                                                          

θ_o represents temperature difference between the fin base and the fluid surrounding the fin.

ii) For a sufficient or infinitely long fin, temperature at the tip of fin is equal to that of surroundings.

At X=L, θ=0                                                                                        (17)

Applying the first boundary condition to equation (2), we get

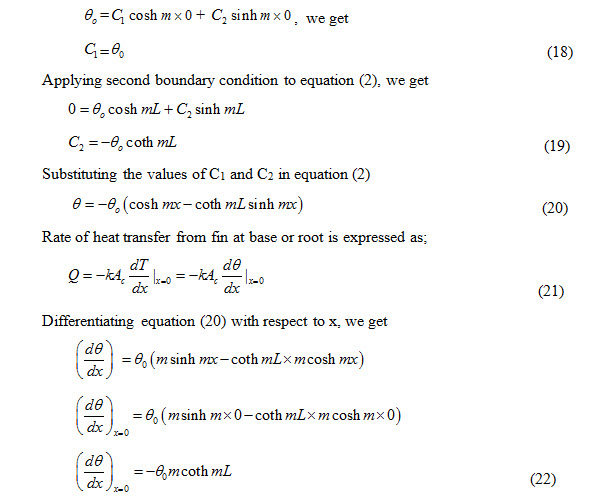
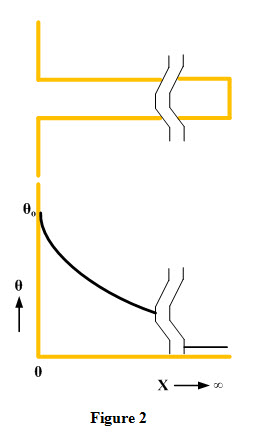
3. Fin is insulated at the tip                                                                                                                                  

For a fin of finite length having its end insulated, no heat transfer takes place from the tip of the fin as shown in Figure 3. The relevant boundary conditions are:

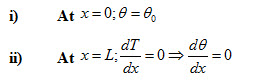
Applying the first boundary conditions to equation (2), we get

c₁ = θ₀                                                                                 (24)

Applying second boundary condition to equation (2), we get

c₂ = -θ₀ tanh mL                                                                (25)   

Substituting the values of C₁ and C₂ in equation (2), we get                             

                                                   

Equation (26) represents temperature distribution in a fin having its end insulated.

Rate of heat transfer from fin at base or root is expressed as;