Reservior & Farm Pond Design 3(2+1)

Lesson 15 Seepage Analysis I

15.2 Permeability of Layered Deposits

Consider the horizontally layered deposit (Fig. 15.1), which consists of pairs of layers the first of which has a permeability of k₁ and a thickness of d₁overlaying a second which has permeability k₂and thickness d₂.

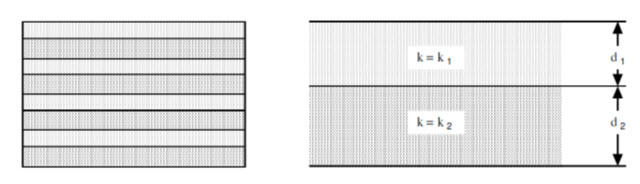
Fig. 15.1. Layered soil. (Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

First consider horizontal flow in the system and suppose that a head difference of ∆h exists between the left and right hand sides (Fig. 15.2).

It then follows from Darcy’s law that,

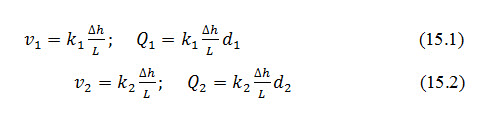
It, therefore, follows:

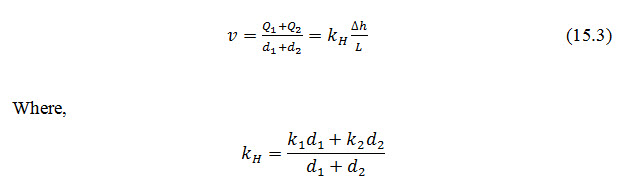
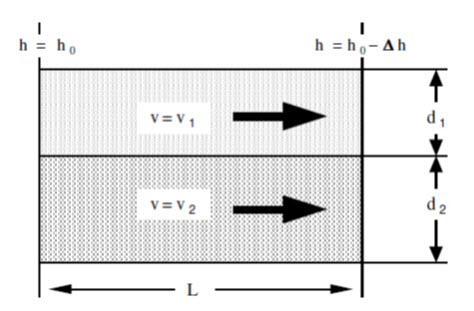
Fig. 15.2. Horizontal flow through layered soil.

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

Next consider vertical flow through the system, shown in fig.15.3. Suppose that the superficial velocity in each of the layers is v and that the head loss in layer 1 is ∆h₁, while the head loss in layer 2 is ∆h₂.

In layer 1:

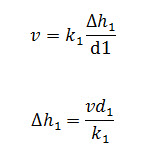
Similarly in layer 2,

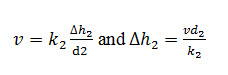
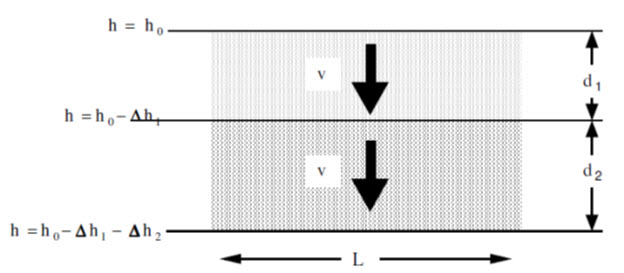
Fig. 15.3. Vertical flow through layered soil.

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

The total head loss across the system will be ∆h=∆h₁+∆h₂ and the hydraulic gradient will be given by,

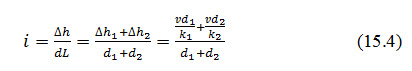
For vertical flow Darcy's law gives,

Total head loss is,          ∆h =, we can write,

15.3 Flow Nets for Soil with Anisotropic Permeability

Flow in a plane in an anisotropic material having a horizontal permeability k_H and a vertical permeability, k_v is governed by the equation:

The solution of this equation can be reduced to that of flow in an isotropic material by the following simple device. Introduce new variables defined as follows:

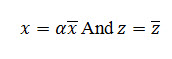
Dividing the equation by, the seepage equation then becomes

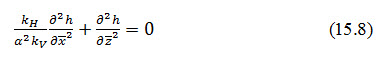
Thus by choosing:

It is found that the equation governing flow in an anisotropic soil reduces to that for an isotropic soil, viz.:

and so the flow in anisotropic soil can be analyzed using the same methods (including sketching flow nets) that are used for analyzing isotropic soils.

15.4 Seepage in Anisotropic Soil: Example

Suppose we wish to calculate the flow under the dam as shown in Fig. 15.4:

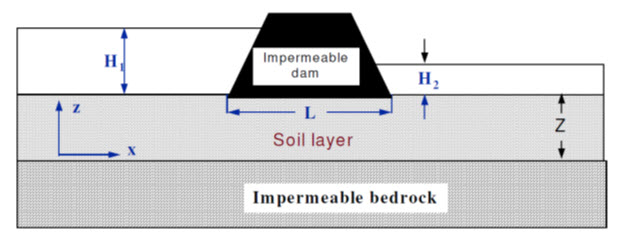
Fig. 15.4. Dam on a permeable soil layer above impermeable rock (natural scale).

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

For the soil shown in Fig.15.4 it is found that k_H= 4k_V. Therefore,

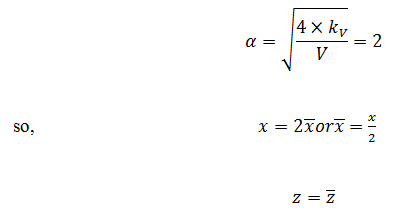
Transformed co-ordinates of a dam on a permeable layer over an impermeable rock and its flow net are shown in Fig.15.5and Fig.15.6, respectively. A rigorous proof of this result will not be given here, but it can be demonstrated to work for purely horizontal flow as:

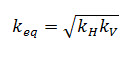
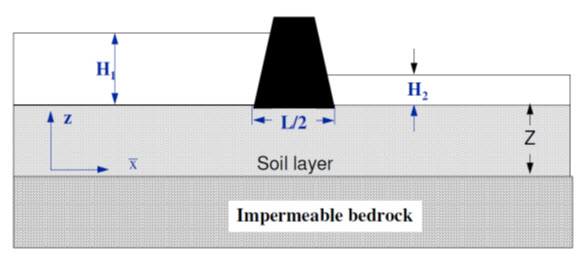
Fig. 15.5. Dam on a permeable layer over impermeable rock (Transformed scale).

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

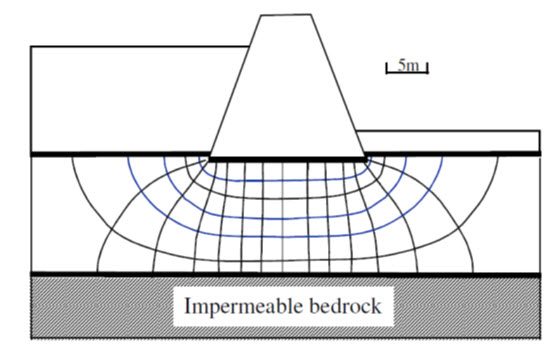
Fig. 15.6. Flow net for transformed geometry.

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

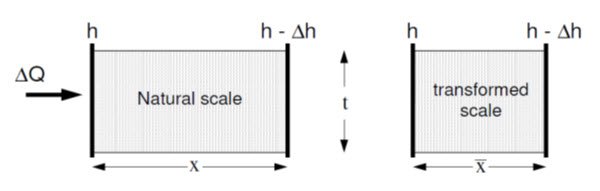
Figure 15.7 shows horizontal flow through anisotropic soil in natural and transformed scale.

Fig. 15.7. Horizontal flow through anisotropic soil.

(Source: https://www.u-cursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

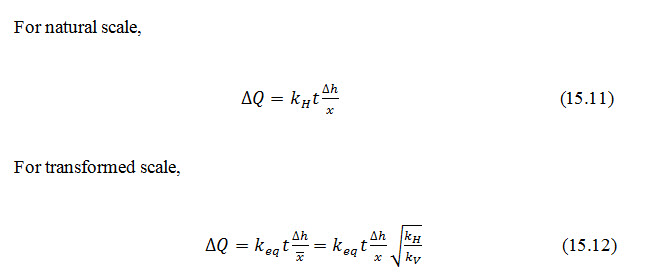
Key words: Anisotropic soil, Flow net, Seepage

References

• Suresh, R. (2002). Soil and Water Conservation Engineering. Fourth Edition. Standard  Publishers.  

• https://www.ucursos.cl/ingenieria/2008/1/CI44A/2/material_docente/objeto/175689.)

Suggested Readings

• http://faculty.washington.edu/jdlund/classes/CEE345/FlowNets/constructing_flow_nets_humboldt_directionsonly.pdf

• http://en.wikipedia.org/wiki/Flownet

• http://faculty.uml.edu/ehajduk/Teaching/14.333/documents/14.3332013FlowNets.pdf

• http://eng.upm.edu.my/webkaw/coursenotes/kaw4313/FlowNets.htm