Reservior & Farm Pond Design 3(2+1)

Lesson 22 Stability Analysis III

 

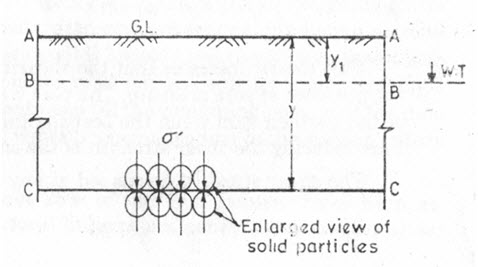
Fig. 22.1. Pore water pressure.

(Source: Garg, 2011)

The soil below BB is fully saturated and all its pores between the solid particles of soil are filled of water. The soil below the water table is, therefore, subjected to hydrostatic uplift. Hence, at any level (say CC), the total downwards normal pressure (s) exerted by the weight of the soil above this level, shall be supported partly by the inter granular pressure (s ors_eff) developed between dry particles of the soil, and partly by the hydrostatic pressure (u) due to the water present in the pores. Hence

Where,= total normal pressure on soil, = total effective pressure, i.e the intergranular pressure, or the pressure which is transmitted from grain to grain of soil, and = pore water pressure or neutral pressure, which is the hydrostatic pressure due to presence of water in the soil pores.

In Fig. 22.1, if the pressures are considered at a level, say CC, at a depth y from the ground, total normal pressure() at level CC is

Where,= depth of water table below the ground level.

Pore water pressure = u

Hence, the net effective pressure (σ') is given by

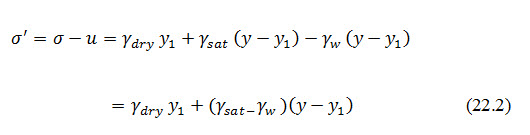
It, therefore, becomes evident that the effective normal stress is much less than the total normal stress, as a part of the total stress gets consumed by water as pore pressure. The effective stress is dependent on the submerged unit weight of soil.

The water pressure or pore pressure acts equally in all directions. It does not press the soil grains against one another, and therefore, does not lead to compression of the soil or an increase in its frictional resistance, that is why, it is called a 'neutral stress'. When the pore pressure is considered, the Coulombs law will become

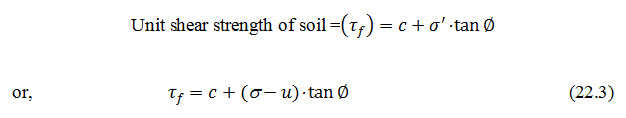
This clearly indicates that the shearing strength of a soil gets reduced due to the presence of pore pressure. The pore water pressure gets developed in the body of the earthen dam when the seepage takes place through the body of the dam, thus reducing the shear strength of the soil. The shear stress developed at any plane in an earth structure is given by

Where, = major principal stress, = minor principal stress, and = angle between the plane considered for shear and the plane on which  acts.

It is apparent from the Eqn. 22.4 that the value of shearing stress remains unaltered, whether and  are used or their effective components[() and(]are used. But the shear strength of the soil gets reduced when effective componentsused in place of s.Hence, the stability of the dam against shear failure must be checked when the maximum pore water pressure is present.

22.2 Consolidation

The development of pore pressure is important, even during the time of construction of an earth dam. When the fully or partly saturated soil is placed and rolled in the body of the dam, the entire applied external load is taken up by the water immediately, and transferred to the soil afterwards. The pore water thus gets compressed, and if it is unable to drain out freely (due to low permeability of the soil) the pore pressure rises. This rise in pore pressure during compaction is known as hydrostatic excess pressure in pore water. It further reduces the shearing strength of the soil and hence, the stability of the soil. As the excess water drains out, more and more consolidation will take place, as this pressure will be transferred to soil grains and the shear strength will tend to achieve its normal value. Hence, the pore pressure temporarily reduces the shear strength of the soil during compaction by preventing full compaction. But the shear strength gets recovered after the compaction is over, as the pore water is ultimately squeezed out.

In highly compressible soils, having low coefficient of permeability and moisture content above its optimum moisture content this condition of hydrostatic excess becomes very serious. Such soils are, therefore, more liable to fail during construction.

Similarly, appreciable consolidation of soil may takes place in fine grained compressible soils like clay, even after the construction is over, though sufficient compaction was done during construction.

Due to these reasons, pore pressure observations are often made during the construction period of an earth dam. If the hydrostatic excess of pore pressure rises to a dangerous level, the construction may be stopped for some time till the excess water drains out and full natural compaction takes place. The construction may be restarted after this excess is either fully dissipated or reduced to a safe value. The shear failure of the soil of the dam or its foundation is, therefore, very much connected with the development of pore pressure in the body of the dam and in the foundation, and must be properly checked and accounted for.

22.3 Stability Charts

The stability chart presented in Fig. 20.5 (lesson 20) affords an accurate and simple method for determining the factor of safety against stability failure for a homogeneous dam and foundation in: (1) the dry condition, (2) the completely submerged condition, (3) the condition of seepage parallel to the face of slope, and (4) the condition of complete rapid drawdown from crown to toe for an embankment with negligible drainage. Approximate solution can be also made for non-homogeneous dams and for the condition of seepage not entirely parallel to the face of the slope and for the condition of rapid drawdown over part of the slope. The chart gives relationship between factor of safety F, height of slope H, angle of slope i, developed friction angle f_D, and developed cohesion c_D.

Keywords: Pore-water pressure, Effective pressure, Seepage, Stability chart

References

• Davis, C.K. (1969). Handbook of Applied Hydraulics. Second Edition. McGraw-Hill, New York.

• Garg, S. K. (2011). Irrigation Engineering and Hydraulic Structures. Khanna Publishers.

Suggested Readings

• Annonymous. (1936) Calculations of the Stability Of Earth Dams, Trans. 2^nd Congress on Large Dams. Washington D.C. 

• Janbu, N. (1954) Stability Analysis of Slopes with Dimensionless Parameters. Harvard  Soil Mechanics Series.