Strength of Material 3(2+1)

LESSON 8. Force Method: Method of Consistent Deformation

8.1.1 Displacement compatibility

It is the condition which ensures the integrability or continuity of different members or components of a loaded structure while being deformed.

Example 1

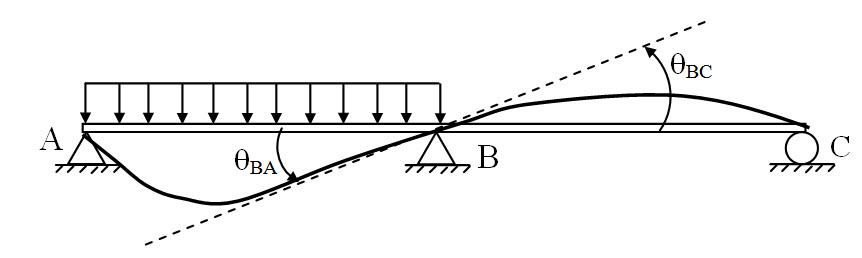
Fig. 8.1.

For the continuous beam shown in Figure 8.1, displacement compatibility conditions at B are,

δ_B = 0 and |θ_BA| = |θ_BC|

The second condition implies that the relative rotation at B is zero.

Example 2

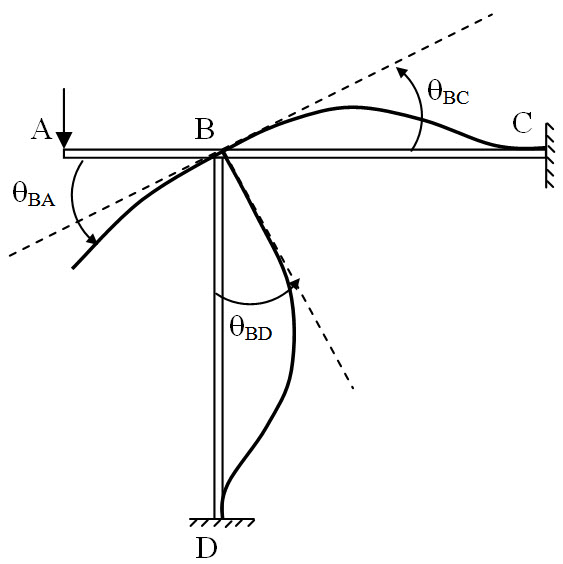
Fig. 8.2.

For the rigid frame shown in Figure 8.2, displacement compatibility conditions at B are,

θ_BA = θ_BC = θ_BD

8.1.2 Principle of Superposition

For a linear elastic structure, the deflection caused by two or more loads acting simultaneously is the sum of deflections caused by each load separately. For instance, suppose d be the deflection at mid-span of a simply supported beam subjected to three concentrated load P₁, P₂ and P₃ (Figure 8.3a).  If δ₁, δ₂, and δ₃ are the deflection at mid-span respectively due to P₁, P₂, and P₃ when they act separately, principle of superposition states,

δ = δ₁+ δ₂ + δ₃

Fig. 8.3a.

For a linear elastic structure, load, P and deflection, δ , are related through stiffness, K, as P = Kδ. If δ₁ and δ₂ are the deflection due to P₁ and P₂ respectively, linearity implies, P₁/P₂ = δ₁/δ₂ .

8.2 General Procedure

Consider a propped cantilever beam subjected to a concentrated load at its mid-span as shown in Figure 8.4. It is an indeterminate structure with degree of static indeterminacy one.

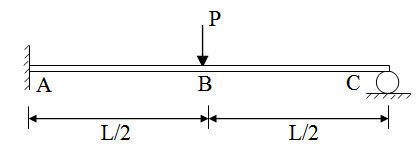
Fig. 8.4.

 The steps involved in method of consistent deformation are as follows,

Step 1: Determine the Degree of Static Indeterminacy

The static indeterminacy of the propped cantilever beam is one.

Step 2: Redundant Force/Moment

A number of releases equal to the degree of indeterminacy is introduced. Each release is made by removing an external or an internal force/moment. This force/moment is called redundant force/moment. Redundant forces/moment should be chosen such that the remaining structure is stable and statically determinate.

For the given propped cantilever beam, the basic determinate structure may be obtained by removing the prop at C (Figure 8.5). Here vertical reaction C_y is the redundant force. The basic determinate structure becomes a cantilever beam with concentrated load at mid-span

 

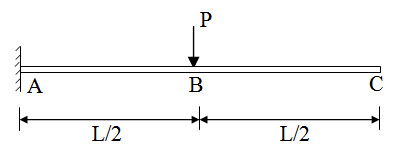
Fig. 8.5.

Alternatively moment constraint at A may also be taken as Redundant. This is explained in sub-section 1.2.1.

Step 3: Solution of Basis Determinate Structure

Calculate the magnitude of the displacement at the released end of the basic determinate structure. Any analysis procedure for determinate structure as discussed in Module I may be followed.

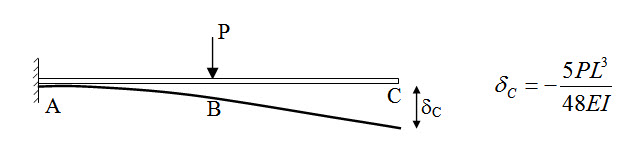
Fig. 8.6.

Here determine vertical displacement at C.

Step 4: Deflection due to Unknown Redundant Force/Moment

Remove all external loads on the basic determinate structure and apply an unknown value of redundant force/moment at the release end. Determine corresponding displacement at the release end in terms of the unknown value of redundant force/moment.

In this case apply vertical force at C and determine δ_C (Figure 8.7).

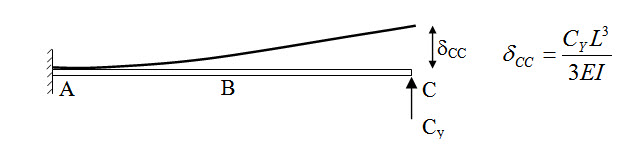
Fig. 8.7.

 Step 5: Apply Compatibility Condition at the Release End

Apply displacement compatibility condition at the release end.

In this case vertical displacement at C is zero. Therefore,

\[{\delta _C}+{\delta _{CC}}=0\Rightarrow-{{5P{L^3}}\over {48EI}}+{{{C_Y}{L^3}}\over {3EI}}=0\Rightarrow{C_Y}={{5P}\over{16}}\]

Step 6: Solve for Other Unknown

Once the redundant force/moment is determined, other support reaction may be found by using equilibrium equations.

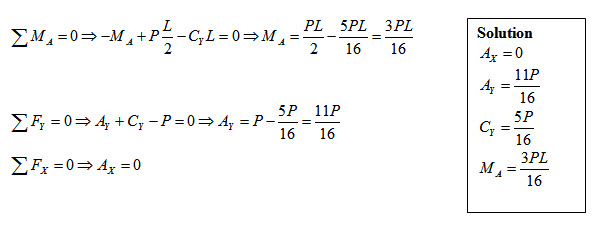
8.2.1 Alternative Solution with Different Redundant Force/Moment

Step 1:

Degree of Static Indeterminacy is one.

Step 2:

Moment constraint at A is taken as redundant. The basic determinate structure becomes a simply supported beam with concentrated load at mid-span (Figure 8.8).

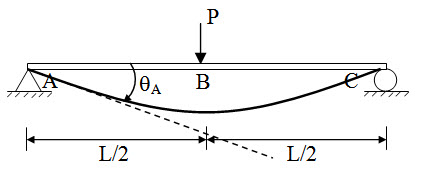
Fig. 8.8.

Step 3:

\[{\theta _A}={{P{L^2}} \over {16EI}}\]

Step 4:

Apply moment M_A at A and calculate slope θ_AA.

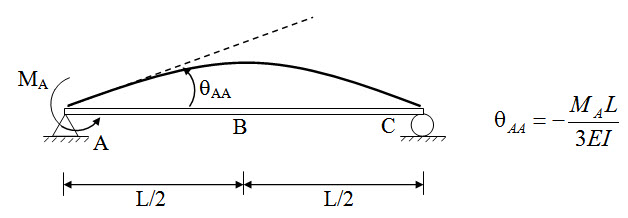
Fig. 8.9.

Step 5:

End A in the original structure is fixed and therefore slope at A is zero.

\[{\theta _A} + {\theta _{AA}}=0 \Rightarrow {{P{L^2}} \over {16EI}}-{{{M_A}L} \over {3EI}}=0 \Rightarrow {M_A}={{3PL} \over {16}}\]

Step 6:

 

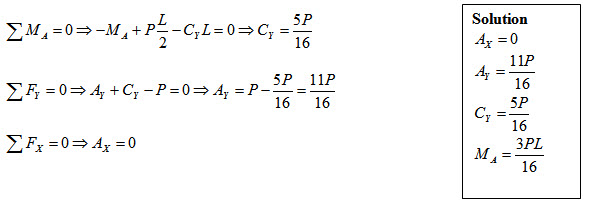
8.3 Maxwell-Betti Reciprocal Theorem

Consider two points 1 and 2 in a simply supported beam as shown in Figure 8.10. The beam is separately subjected to two system of forces P₁ and P₂ at point 1 and 2 respectively. Let d₁₂ be the deflection at point 2 due to P₁ acting at point 1 (Figure 8.10a) and d₂₁ be the deflection at point 1 due to P₂ acting at point 2 Figure 8.10b).

Fig.8.10 (a)                                                                               Fig.8.10 (b)

The Reciprocal theorem states, the work done by the first system of forces acting through the displacement of second system is the same as the work done by the second system of forces acting through the displacement of first system. Therefore,

\[{P_1}\times{\delta _{21}}={P_2}\times {\delta _{12}}\]

The reciprocal theorem is also valid for moment-rotation system. For instance, for the system shown in Figure 8.11, the reciprocal theorem gives,

\[{M_1} \times {\theta _{21}}={M_2} \times {\theta _{12}}\]

Fig. 8.11.

 

Suggested Readings

Hbbeler, R. C. (2002). Structural Analysis, Pearson Education (Singapore) Pte. Ltd.,Delhi.

Jain, A.K., Punmia, B.C., Jain, A.K., (2004). Theory of Structures. Twelfth Edition, Laxmi Publications. 

Menon, D.,  (2008), Structural Analysis, Narosa Publishing House Pvt. Ltd., New Delhi.

Hsieh, Y.Y., (1987), Elementry Theory of Structures , Third Ddition, Prentrice Hall.