Site pages
Current course
Participants
General
MODULE 1. Analysis of Statically Determinate Beams
MODULE 2. Analysis of Statically Indeterminate Beams
MODULE 3. Columns and Struts
MODULE 4. Riveted and Welded Connections
MODULE 5. Stability Analysis of Gravity Dams
Keywords
LESSON 10. Force Method: Beams on Elastic Support
In many application, beams are required to be supported on a continous foundation. One such example is railway sleeper as shwon in Figure 10.1. If the reaction force offered by such continuous support is a function of the transverse deflection of the beam, the support is called elastic support. In this lesson we will learn analysis procedure of beam resting on elastic support.
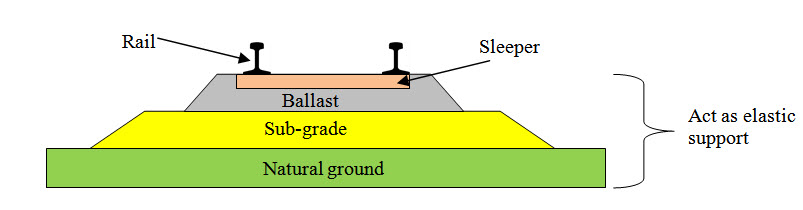
Fig. 10.1.
10.1 Formulation of Governing Equation
Consider a beam, resting on an elastic support, is subjected to any arbitrary load as shwon in Figure 10.2a. Support reaction which is a function of the transverse displacement is shwon in Figure 10.2b
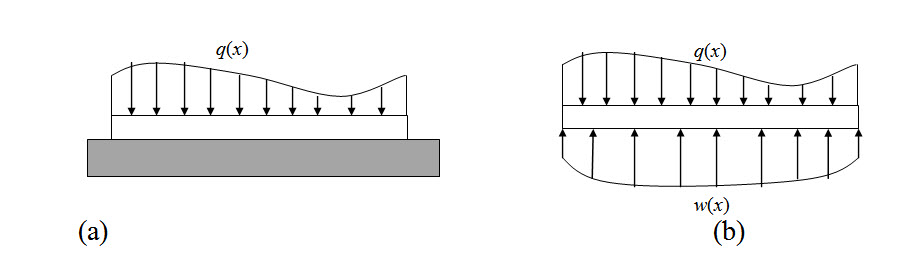
Fig. 10.2.
The reaction offered by the support is a linear funciton of displacement and may be written as,
\[w(x) = ky(x)\]
where, the constant k is the stiffness of the elastic foundation. Therefore at any location x, the net intensity of load is \[q(x) - ky(x)\] . Consequently the equation of elastic line, derived in lesson 3 (Equation 3.11) becomes,
\[{{{d^2}} \over {d{x^2}}}\left( {EI{{{d^2}y} \over {d{x^2}}}} \right) = q(x) - ky(x)\] (10.1)
For a beam with uniform cross-section and material property, taking EI out from the defferential operator, equation (10.1) becomes,
\[{{{d^4}y} \over {d{x^4}}} + 4{\beta ^4}y = q\] , (10.2)
Where, \[{\beta ^4} = {k \over {4EI}}\]
The above equation is the differential equation for beam on elastic support.
In absence of any external load, the homogeneous form may be written as,
\[{{{d^4}y} \over {d{x^4}}} + 4{\beta ^4}y = 0\] (10.3)
The general solution of above homogeneous differential equation is,
\[y(x) = {e^{\beta x}}\left( {{C_1}\sin \beta x + {C_2}\cos \beta x} \right) + {e^{ - \beta x}}\left( {{C_3}\sin \beta x + {C_4}\cos \beta x} \right)\]
10.1 Semi-infinite beam with concentrated load

Fig.10.3.
The general solution of above homogeneous differential equation is,
\[y(x) = {e^{\beta x}}\left( {{C_1}\sin \beta x + {C_2}\cos \beta x} \right) + {e^{ - \beta x}}\left( {{C_3}\sin \beta x + {C_4}\cos \beta x} \right)\]
Now, for \[x \to \infty\] , y = 0 \[\Rightarrow {e^{\beta x}}\left( {{C_1}\sin \beta x + {C_2}\cos \beta x} \right) = 0\]
\[y(x) = {e^{ - \beta x}}\left( {{C_3}\sin \beta x + {C_4}\cos \beta x} \right)\]
Boundary conditions,
\[M(x = 0) = {M_0}\] and \[V(x = 0) =-{P_0}\]
From lesson 3, we have other forms of equations of elastic line as,
\[{{{d^2}y} \over {d{x^2}}} =-{M \over {EI}}\] and \[{{{d^3}y} \over {d{x^3}}}=-{V \over {EI}}\]
Combining the above equations with the boundary conditions, we have,
\[{\left. {{{{d^2}y} \over {d{x^2}}}} \right|_{x = 0}} =-{{{M_0}} \over {EI}}\] and \[{\left. {{{{d^3}y} \over {d{x^3}}}} \right|_{x = 0}} = {{{P_0}} \over {EI}}\]
\[{{{d^2}y} \over {d{x^2}}} =-2{\beta ^2}{C_3}{e^{ - \beta x}}\cos \beta x + 2{\beta ^2}{C_4}{e^{ - \beta x}}\sin \beta x\]
\[{{{d^3}y} \over {d{x^3}}} = 2{\beta ^3}{C_3}{e^{ - \beta x}}\cos \beta x - 2{\beta ^3}{C_4}{e^{ - \beta x}}\sin \beta x + 2{\beta ^3}{C_3}{e^{ - \beta x}}\sin \beta x + 2{\beta ^3}{C_4}{e^{ - \beta x}}\cos \beta x\]
\[{\left. {{{{d^2}y} \over {d{x^2}}}} \right|_{x = 0}} =-2{\beta ^2}{C_3} =-{{{M_0}} \over {EI}} \Rightarrow {C_3} = {{{M_0}} \over {2EI{\beta ^2}}}\]
\[{\left. {{{{d^3}y} \over {d{x^3}}}} \right|_{x = 0}} = 2{\beta ^3}{C_3} + 2{\beta ^3}{C_4} = {{{P_0}} \over {EI}} \Rightarrow {C_4} = {{{P_0}} \over {2EI{\beta ^3}}} - {{{M_0}} \over {2EI{\beta ^2}}}\]
Final solution
\[y(x) = {{{e^{ - \beta x}}} \over {2EI{\beta ^2}}}\left[ {{M_0}\left( {\sin \beta x - \cos \beta x} \right) + {{{P_0}} \over {2EI{\beta ^3}}}\cos \beta x} \right]\]
\[M(x) =-EI{{{d^2}y} \over {d{x^2}}}\] ; \[V(x) =-EI{{{d^3}y} \over {d{x^3}}}\]
Suggested Readings
Hbbeler, R. C. (2002). Structural Analysis, Pearson Education (Singapore) Pte. Ltd.,Delhi.
Jain, A.K., Punmia, B.C., Jain, A.K., (2004). Theory of Structures. Twelfth Edition, Laxmi Publications.
Menon, D., (2008), Structural Analysis, Narosa Publishing House Pvt. Ltd., New Delhi.
Hsieh, Y.Y., (1987), Elementry Theory of Structures , Third Ddition, Prentrice Hall.